Question Number 130725 by mathmax by abdo last updated on 28/Jan/21

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}}\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Jan/21
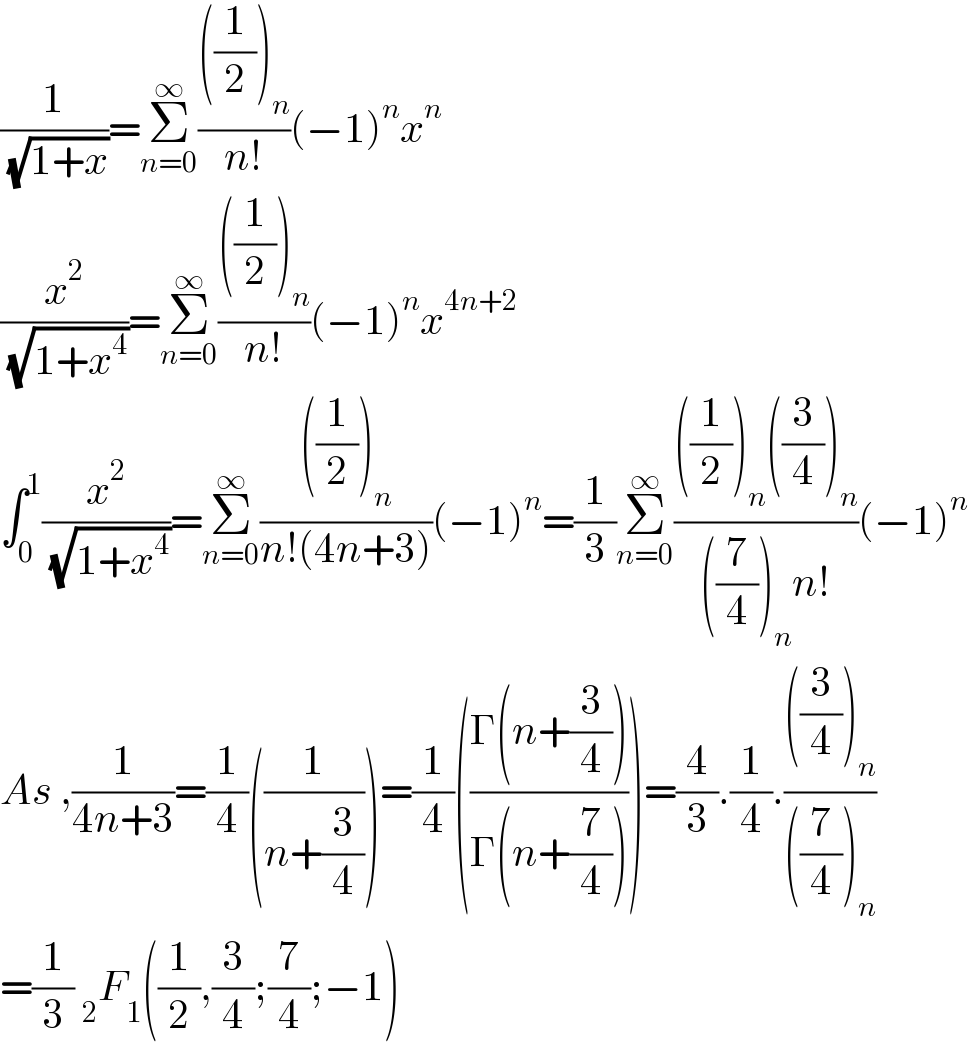
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \\ $$$$\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{4}{n}+\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!\left(\mathrm{4}{n}+\mathrm{3}\right)}\left(−\mathrm{1}\right)^{{n}} =\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)_{{n}} }{\left(\frac{\mathrm{7}}{\mathrm{4}}\right)_{{n}} {n}!}\left(−\mathrm{1}\right)^{{n}} \\ $$$${As}\:,\frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{n}+\frac{\mathrm{3}}{\mathrm{4}}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{4}}\right)}{\Gamma\left({n}+\frac{\mathrm{7}}{\mathrm{4}}\right)}\right)=\frac{\mathrm{4}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{4}}.\frac{\left(\frac{\mathrm{3}}{\mathrm{4}}\right)_{{n}} }{\left(\frac{\mathrm{7}}{\mathrm{4}}\right)_{{n}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{4}};\frac{\mathrm{7}}{\mathrm{4}};−\mathrm{1}\right) \\ $$
Commented by mathmax by abdo last updated on 28/Jan/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
