find-0-1-x-x-dx-study-first-the-convergence-

Question Number 64528 by mathmax by abdo last updated on 19/Jul/19

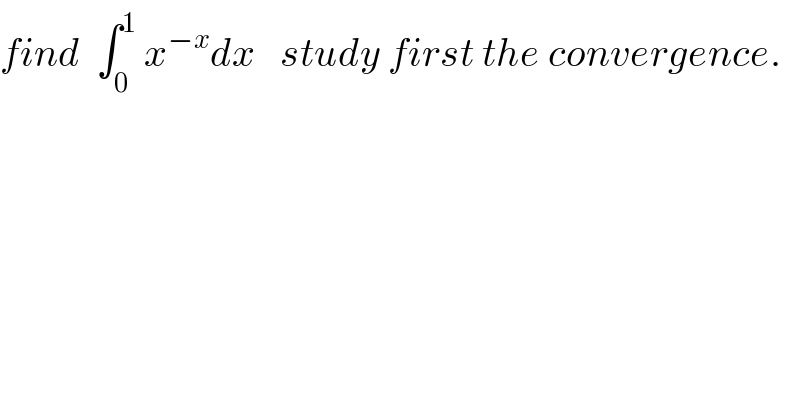
f i n d \int_{0}^{1} x^{- x} d x s t u d y f i r s t t h e c o n v e r g e n c e .

Commented by mathmax by abdo last updated on 19/Jul/19

w e h a v e x^{- x} = e^{- x l n (x)} l e t A = \int_{0}^{1} x^{- x} d x \Rightarrow A = \int_{0}^{1} e^{- x l n x} d x

w e h a v e {l i m}_{x \to 0^{+}} x l n (x) = 0 \Rightarrow {l i m}_{x \to 0^{}} e^{- x l n x} = 1 s o

t h e f u n c t i o n x \to e^{- x l n x} i s i n t e g r a b l e o n [0, 1]

w e h a v e A = \int_{0}^{1} \sum_{n = 0}^{\infty} \frac{{(- x l n x)}^{n}}{n!} d x = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{n!} \int_{0}^{1} x^{n} {(l n x)}^{n} d x

= \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{n!} w_{n}

w_{n} = \int_{0}^{1} x^{n} {(l n x)}^{n} d x =_{l n x = - t} \int_{+ \infty}^{0} e^{- n t} {(- t)}^{n} (- e^{- t}) d t

= \int_{0}^{\infty} {(- 1)}^{n} t^{n} e^{- (n + 1) t} d t =_{(n + 1) t = u} {(- 1)}^{n} \int_{0}^{\infty} \frac{u^{n}}{{(n + 1)}^{n}} e^{- u} \frac{d u}{(n + 1)}

= \frac{{(- 1)}^{n}}{{(n + 1)}^{n + 1}} \int_{0}^{\infty} u^{n} e^{- u} d u w e k n o w t h a t Γ (x) = \int_{0}^{\infty} t^{x - 1} e^{- t} d t \Rightarrow

\int_{0}^{\infty} u^{n} e^{- u} d u = Γ (n + 1) = n! \Rightarrow w_{n} = \frac{{(- 1)}^{n} n!}{{(n + 1)}^{n + 1}} \Rightarrow

A = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{n!} \frac{{(- 1)}^{n} n!}{{(n + 1)}^{n + 1}} = \sum_{n = 0}^{\infty} \frac{1}{{(n + 1)}^{n + 1}} = \sum_{n = 1}^{\infty} \frac{1}{n^{n}}

= 1 + \frac{1}{2^{2}} + \frac{1}{3^{3}} + \frac{1}{4^{4}} + \dots .