Question Number 83383 by mhmd last updated on 01/Mar/20
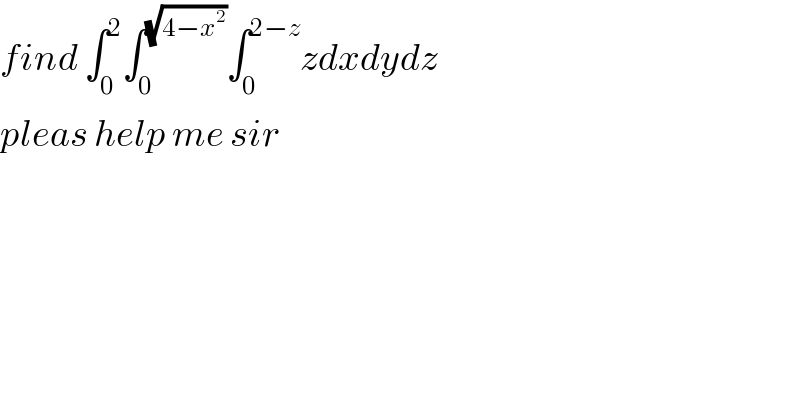
$${find}\:\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \int_{\mathrm{0}} ^{\mathrm{2}−{z}} {zdxdydz} \\ $$$${pleas}\:{help}\:{me}\:{sir} \\ $$
Answered by mr W last updated on 01/Mar/20
![∫_0 ^2 ∫_0 ^(√(4−x^2 )) ∫_0 ^(2−z) zdxdydz =∫_0 ^2 ∫_0 ^(√(4−x^2 )) (∫_0 ^(2−z) zdy)dzdx =∫_0 ^2 (∫_0 ^(√(4−x^2 )) z(2−z)dz)dx =∫_0 ^2 [z^2 −(z^3 /3)]_0 ^(√(4−x^2 )) dx =∫_0 ^2 [4−x^2 −(((4−x^2 )^(3/2) )/3)]dx =4×2−(2^3 /3)−(1/3)∫_0 ^2 (4−x^2 )^(3/2) dx =((16)/3)−(1/3)∫_0 ^2 (4−x^2 )^(3/2) dx =((16)/3)−(1/3)×3π (see below) =((16)/3)−π let x=2 sin θ ∫_0 ^2 (4−x^2 )^(3/2) dx =∫_0 ^(π/2) (4 cos^2 θ)^(3/2) 2 cos θ dθ =16∫_0 ^(π/2) cos^4 θ dθ =4∫_0 ^(π/2) (2 cos^2 θ)^2 dθ =4∫_0 ^(π/2) (1+cos 2θ)^2 dθ =4∫_0 ^(π/2) (1+2 cos 2θ+cos^2 2θ) dθ =4∫_0 ^(π/2) (1+2 cos 2θ+((1+cos 4θ)/2)) dθ =4∫_0 ^(π/2) ((3/2)+2 cos 2θ+((cos 4θ)/2)) dθ =4[(3/2)θ+sin 2θ+((sin 4θ)/8)]_0 ^(π/2) =4×(3/2)×(π/2) =3π](https://www.tinkutara.com/question/Q83393.png)
$$\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \int_{\mathrm{0}} ^{\mathrm{2}−{z}} {zdxdydz} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \left(\int_{\mathrm{0}} ^{\mathrm{2}−{z}} {zdy}\right){dzdx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\int_{\mathrm{0}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} {z}\left(\mathrm{2}−{z}\right){dz}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left[{z}^{\mathrm{2}} −\frac{{z}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left[\mathrm{4}−{x}^{\mathrm{2}} −\frac{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}\right]{dx} \\ $$$$=\mathrm{4}×\mathrm{2}−\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} {dx} \\ $$$$=\frac{\mathrm{16}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} {dx} \\ $$$$=\frac{\mathrm{16}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{3}\pi\:\:\:\left({see}\:{below}\right) \\ $$$$=\frac{\mathrm{16}}{\mathrm{3}}−\pi \\ $$$$ \\ $$$${let}\:{x}=\mathrm{2}\:\mathrm{sin}\:\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{2}\:\mathrm{cos}\:\theta\:{d}\theta \\ $$$$=\mathrm{16}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{4}} \:\theta\:{d}\theta \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} \:{d}\theta \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)^{\mathrm{2}} \:{d}\theta \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta\right)\:{d}\theta \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta+\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{4}\theta}{\mathrm{2}}\right)\:{d}\theta \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta+\frac{\mathrm{cos}\:\mathrm{4}\theta}{\mathrm{2}}\right)\:{d}\theta \\ $$$$=\mathrm{4}\left[\frac{\mathrm{3}}{\mathrm{2}}\theta+\mathrm{sin}\:\mathrm{2}\theta+\frac{\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{8}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{4}×\frac{\mathrm{3}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}} \\ $$$$=\mathrm{3}\pi \\ $$
