Question Number 31076 by abdo imad last updated on 02/Mar/18
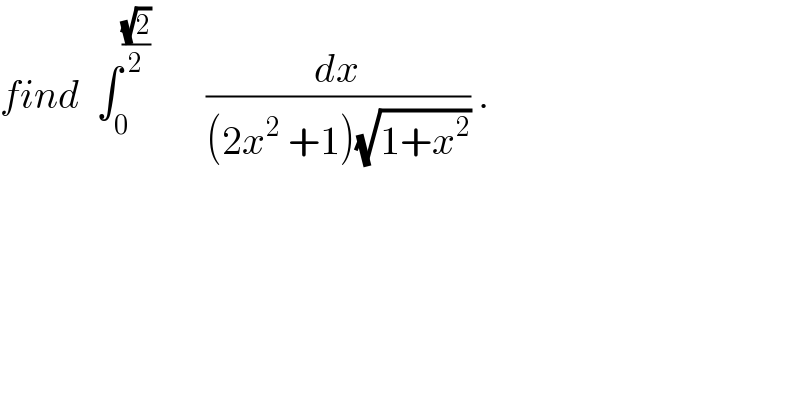
$${find}\:\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \:\:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:. \\ $$
Commented by abdo imad last updated on 07/Mar/18
![the ch.x=sht give I= ∫_0 ^(argsh(((√2)/2))) ((cht dt)/((2 sh^2 t +1)cht))=∫_0 ^(argsh(((√2)/2))) (dt/(2sh^2 t +1)) sh^2 t= (((e^t −e^(−t) )/2))^2 =(1/4)(e^(2t) +e^(−2t) −2)⇒2sh^2 t=(1/2)( e^(2t) +e^(−2t) −2) =((e^(2t) +e^(−2t) )/2) −1 ⇒ 2sh^2 t +1 = ((e^(2t) +e^(−2t) )/2) ⇒ I = ∫_0 ^(argsh(((√2)/2))) ((2dt)/(e^(2t) +e^(−2t) )) let use tbe chan. e^(2t) =u ⇒2t=lnu I= ∫_1 ^e^(2argh(((√2)/2))) (2/(u +(1/u))) (du/(2u))=∫_1 ^e^(2argsh(((√2)/2))) (du/(1+u^2 ))=[arctanu]_1 ^e^(2argsh(((√2)/2))) but we have argshx=ln(x+(√(1+x^2 ))) ⇒ argsh(((√2)/2))=ln( ((√2)/2) +(√(3/2)) )⇒2argsh(((√2)/2))=ln((((√2)/2) +((√3)/( (√2))))^2 ) and e^(2argsh(((√2)/2))) = (1/2) +(√3) +(3/2)=2+(√3) ⇒ I= arctan(2+(√3)) −(π/4) .](https://www.tinkutara.com/question/Q31397.png)
$${the}\:{ch}.{x}={sht}\:{give}\: \\ $$$${I}=\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)} \:\:\:\:\frac{{cht}\:{dt}}{\left(\mathrm{2}\:{sh}^{\mathrm{2}} {t}\:+\mathrm{1}\right){cht}}=\int_{\mathrm{0}} ^{{argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)} \:\:\:\:\frac{{dt}}{\mathrm{2}{sh}^{\mathrm{2}} {t}\:+\mathrm{1}} \\ $$$${sh}^{\mathrm{2}} {t}=\:\left(\frac{{e}^{{t}} \:−{e}^{−{t}} }{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left({e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} \:−\mathrm{2}\right)\Rightarrow\mathrm{2}{sh}^{\mathrm{2}} {t}=\frac{\mathrm{1}}{\mathrm{2}}\left(\:{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} −\mathrm{2}\right) \\ $$$$=\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\:−\mathrm{1}\:\Rightarrow\:\mathrm{2}{sh}^{\mathrm{2}} {t}\:+\mathrm{1}\:=\:\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)} \:\:\frac{\mathrm{2}{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }\:\:{let}\:{use}\:{tbe}\:{chan}.\:{e}^{\mathrm{2}{t}} ={u}\:\Rightarrow\mathrm{2}{t}={lnu} \\ $$$${I}=\:\int_{\mathrm{1}} ^{{e}^{\mathrm{2}{argh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)} } \:\:\frac{\mathrm{2}}{{u}\:+\frac{\mathrm{1}}{{u}}}\:\:\frac{{du}}{\mathrm{2}{u}}=\int_{\mathrm{1}} ^{{e}^{\mathrm{2}{argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)} } \:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }=\left[{arctanu}\right]_{\mathrm{1}} ^{{e}^{\mathrm{2}{argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)} } \:\:\:{but} \\ $$$${we}\:{have}\:{argshx}={ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)={ln}\left(\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:\right)\Rightarrow\mathrm{2}{argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)={ln}\left(\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:+\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \right) \\ $$$${and}\:{e}^{\mathrm{2}{argsh}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)} =\:\frac{\mathrm{1}}{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:+\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{2}+\sqrt{\mathrm{3}}\:\:\Rightarrow \\ $$$${I}=\:{arctan}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\:−\frac{\pi}{\mathrm{4}}\:. \\ $$
