Question Number 90171 by M±th+et£s last updated on 21/Apr/20
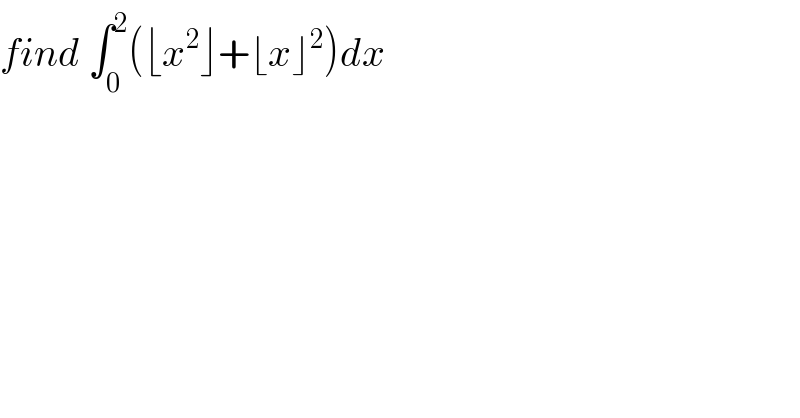
$${find}\:\int_{\mathrm{0}} ^{\mathrm{2}} \left(\lfloor{x}^{\mathrm{2}} \rfloor+\lfloor{x}\rfloor^{\mathrm{2}} \right){dx} \\ $$
Answered by TANMAY PANACEA. last updated on 21/Apr/20
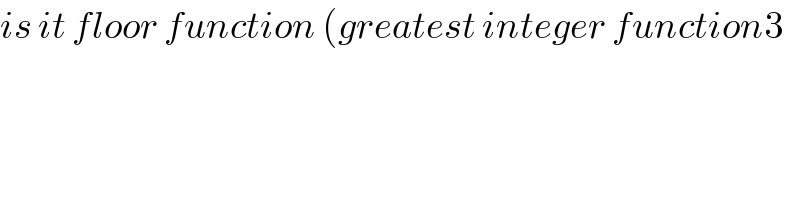
$${is}\:{it}\:{floor}\:{function}\:\left({greatest}\:{integer}\:{function}\mathrm{3}\right. \\ $$
Commented by M±th+et£s last updated on 21/Apr/20

$${yes}\:{sir} \\ $$
Answered by TANMAY PANACEA. last updated on 21/Apr/20
![∫_0 ^1 [x^2 ]dx+∫_1 ^(√2) [x^2 ]dx+∫_(√2) ^(√3) [x^2 ]dx+∫_(√3) ^2 [x^2 ]dx =∫_0 ^1 0.dx+∫_1 ^(√2) 1.dx+∫_(√2) ^(√3) 2.dx+∫_(√3) ^2 3.dx =0.2)+1.((√2) −1)+2((√3) −(√2) )+3(2−(√3) ) =0+(√2) −1+2(√3) −2(√2) +6−3(√3) =5−(√2) −(√3) ∫_0 ^2 [x]^2 dx ∫_0 ^1 0×dx+∫_1 ^2 1×dx =1 Answer=5−(√2) −(√3) +1 =6−(√2) −(√3)](https://www.tinkutara.com/question/Q90174.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left[{x}^{\mathrm{2}} \right]{dx}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \left[{x}^{\mathrm{2}} \right]{dx}+\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \left[{x}^{\mathrm{2}} \right]{dx}+\int_{\sqrt{\mathrm{3}}} ^{\mathrm{2}} \left[{x}^{\mathrm{2}} \right]{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{0}.{dx}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \mathrm{1}.{dx}+\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\mathrm{2}.{dx}+\int_{\sqrt{\mathrm{3}}} ^{\mathrm{2}} \mathrm{3}.{dx} \\ $$$$\left.=\mathrm{0}.\mathrm{2}\right)+\mathrm{1}.\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)+\mathrm{2}\left(\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}\:\right)+\mathrm{3}\left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right) \\ $$$$=\mathrm{0}+\sqrt{\mathrm{2}}\:−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\:−\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{6}−\mathrm{3}\sqrt{\mathrm{3}}\: \\ $$$$=\mathrm{5}−\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \left[{x}\right]^{\mathrm{2}} {dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{0}×{dx}+\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{1}×{dx} \\ $$$$=\mathrm{1} \\ $$$${Answer}=\mathrm{5}−\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}\:+\mathrm{1} \\ $$$$=\mathrm{6}−\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}\: \\ $$
Commented by M±th+et£s last updated on 21/Apr/20
$${nice}\:{work}\:{sir}\:{thank}\:{you} \\ $$
Commented by TANMAY PANACEA. last updated on 21/Apr/20

$${most}\:{welcome}\:{sir} \\ $$
