Menu Close

find-0-2pi-dx-3cosx-2-

Tinku Tara 0 Comments
Pin




Question Number 92937 by mathmax by abdo last updated on 09/May/20
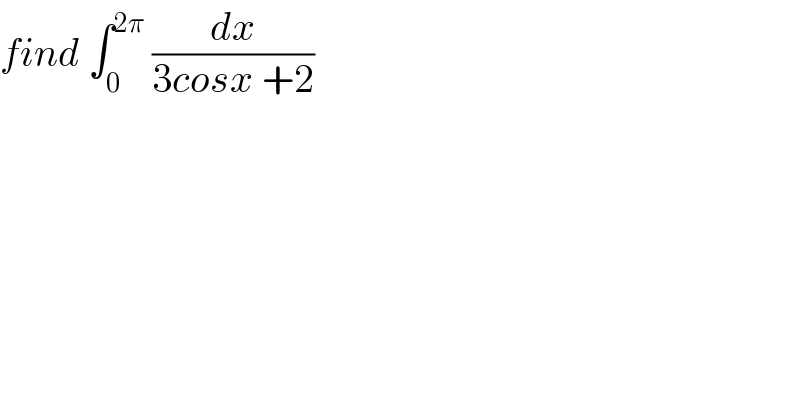
find ∫_0 ^(2π) (dx/(3cosx +2))
$${find}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\mathrm{3}{cosx}\:+\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 10/May/20
A =∫_0 ^(2π) (dx/(3cosx +2)) cha7gement e^(ix) =z give A =∫_(∣z∣=1) (dz/(iz(3((z+z^(−1) )/2)+2))) =∫_(∣z∣=1) ((−2i dz)/(z(3z +3z^(−1) +4))) =∫_(∣z∣=1) ((−2idz)/(3z^2 +3+4z)) let ϕ(z) =((−2i)/(3z^2 +4z+3)) poles of ϕ? 3z^2 +4z +3 =0→Δ^′ =4−9 =−5 ⇒z_1 =((−2+i(√5))/3) z_2 =((−2−i(√5))/3) ⇒ϕ(z) =((−2i)/(3(z−z_1 )(z−z_2 ))) ∣z_1 ∣−1 =(1/3)(√9)=1 and ∣z_2 ∣−1 =1 residus theorem give ∫_(∣z∣=1) ϕ(z)dz =2iπ { Res(ϕ,z_1 )+Res(ϕ,z_2 )} Res(ϕ,z_1 ) =((−2i)/3)×(3/(2i(√5))) =((−1)/( (√5))) Res(ϕ,z_2 ) =((−2i)/3)×((−3)/(2i(√5))) =(1/( (√5))) ⇒∫_(∣z∣=1) ϕ(z)dz =0 ⇒A =0
$${A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\mathrm{3}{cosx}\:+\mathrm{2}}\:{cha}\mathrm{7}{gement}\:\:{e}^{{ix}} \:={z}\:{give} \\ $$$${A}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{{dz}}{{iz}\left(\mathrm{3}\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}+\mathrm{2}\right)}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{2}{i}\:{dz}}{{z}\left(\mathrm{3}{z}\:+\mathrm{3}{z}^{−\mathrm{1}} \:+\mathrm{4}\right)} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{2}{idz}}{\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{3}+\mathrm{4}{z}}\:\:{let}\:\varphi\left({z}\right)\:=\frac{−\mathrm{2}{i}}{\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{4}{z}+\mathrm{3}}\:\:{poles}\:{of}\:\varphi? \\ $$$$\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{4}{z}\:+\mathrm{3}\:=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{4}−\mathrm{9}\:=−\mathrm{5}\:\Rightarrow{z}_{\mathrm{1}} =\frac{−\mathrm{2}+{i}\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${z}_{\mathrm{2}} =\frac{−\mathrm{2}−{i}\sqrt{\mathrm{5}}}{\mathrm{3}}\:\Rightarrow\varphi\left({z}\right)\:=\frac{−\mathrm{2}{i}}{\mathrm{3}\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$$\mid{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{9}}=\mathrm{1}\:\:{and}\:\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\mathrm{1}\:{residus}\:{theorem}\:{give} \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right)+{Res}\left(\varphi,{z}_{\mathrm{2}} \right)\right\} \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:=\frac{−\mathrm{2}{i}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{2}{i}\sqrt{\mathrm{5}}}\:=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${Res}\left(\varphi,{z}_{\mathrm{2}} \right)\:=\frac{−\mathrm{2}{i}}{\mathrm{3}}×\frac{−\mathrm{3}}{\mathrm{2}{i}\sqrt{\mathrm{5}}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\Rightarrow\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\varphi\left({z}\right){dz}\:=\mathrm{0}\:\Rightarrow{A}\:=\mathrm{0} \\ $$
Answered by john santu last updated on 10/May/20
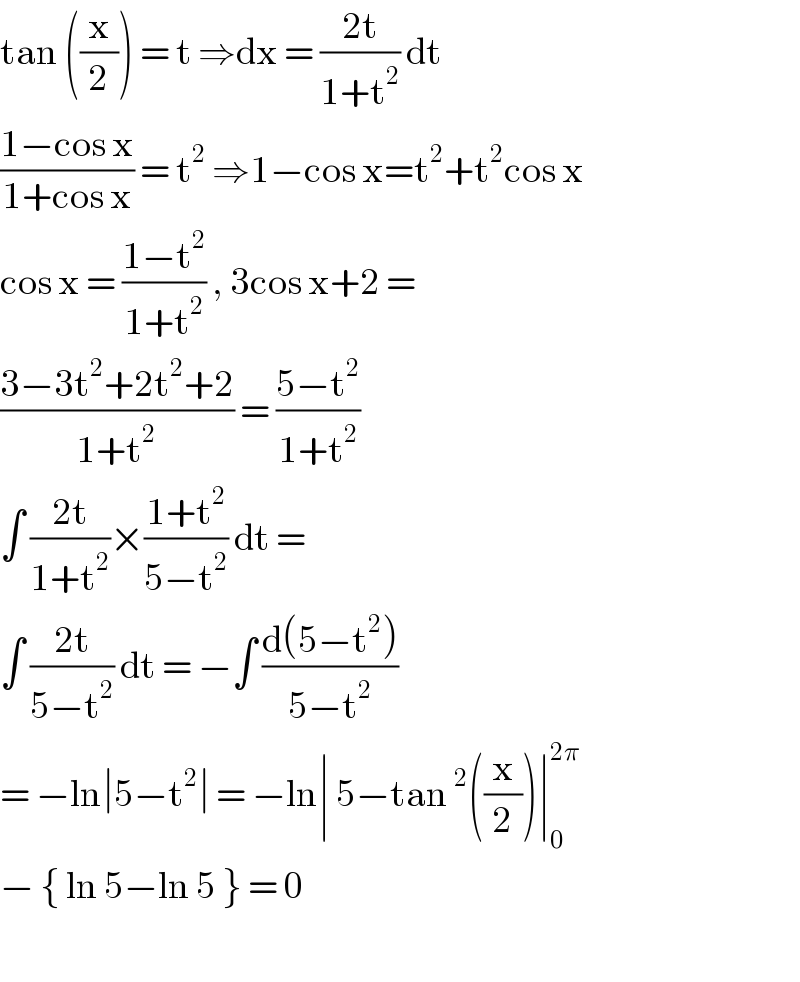
tan ((x/2)) = t ⇒dx = ((2t)/(1+t^2 )) dt ((1−cos x)/(1+cos x)) = t^2 ⇒1−cos x=t^2 +t^2 cos x cos x = ((1−t^2 )/(1+t^2 )) , 3cos x+2 = ((3−3t^2 +2t^2 +2)/(1+t^2 )) = ((5−t^2 )/(1+t^2 )) ∫ ((2t)/(1+t^2 ))×((1+t^2 )/(5−t^2 )) dt = ∫ ((2t)/(5−t^2 )) dt = −∫ ((d(5−t^2 ))/(5−t^2 )) = −ln∣5−t^2 ∣ = −ln∣ 5−tan^2 ((x/2))∣_0 ^(2π) − { ln 5−ln 5 } = 0
$$\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\mathrm{t}\:\Rightarrow\mathrm{dx}\:=\:\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\:=\:\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{1}−\mathrm{cos}\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:,\:\mathrm{3cos}\:\mathrm{x}+\mathrm{2}\:=\: \\ $$$$\frac{\mathrm{3}−\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}^{\mathrm{2}} +\mathrm{2}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\:\frac{\mathrm{5}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\int\:\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }×\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{5}−\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:= \\ $$$$\int\:\frac{\mathrm{2t}}{\mathrm{5}−\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:=\:−\int\:\frac{\mathrm{d}\left(\mathrm{5}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{5}−\mathrm{t}^{\mathrm{2}} } \\ $$$$=\:−\mathrm{ln}\mid\mathrm{5}−\mathrm{t}^{\mathrm{2}} \mid\:=\:−\mathrm{ln}\mid\:\mathrm{5}−\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$−\:\left\{\:\mathrm{ln}\:\mathrm{5}−\mathrm{ln}\:\mathrm{5}\:\right\}\:=\:\mathrm{0} \\ $$$$ \\ $$
Answered by niroj last updated on 10/May/20
I= ∫_0 ^( 2π) (dx/(3cos x+2)) = [ ∫ (dx/(3(((1−tan^2 (x/2))/(1+tan^2 (x/2))))+2))]_0 ^(2π) = [ ∫ (( dx)/((3−3tan^2 (x/2)+2+2tan^2 (x/2))/(1+tan^2 (x/2))))]^(2π) _0 = [ ∫ ((sec^2 (x/2) dx)/(5−tan^2 (x/2)))]_0 ^(2π) Put, tan (x/2) = t sec^2 (x/2)dx=2dt [ ∫ ((2dt)/(5−t^2 ))]_0 ^(2π) = [ 2∫ (1/(((√5) )^2 −(t)^2 ))dt]_0 ^(2π) [ 2.(1/(2(√5)))log (( (√5) +t)/( (√5) −t)) ]_0 ^(2π) = ((1/( (√5)))log (( (√5) + tan(x/2))/( (√5) −tan(x/2))))−((1/( (√5)))log ((√5)/( (√5)))) =0 //.
$$\:\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \:\frac{{dx}}{\mathrm{3}{cos}\:{x}+\mathrm{2}} \\ $$$$\:\:\:=\:\left[\:\int\:\frac{\mathrm{dx}}{\mathrm{3}\left(\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}\right)+\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:=\:\left[\:\int\:\frac{\:\:\mathrm{dx}}{\frac{\mathrm{3}−\mathrm{3tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}+\mathrm{2}+\mathrm{2tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}}\underset{\mathrm{0}} {\right]}^{\mathrm{2}\pi} \\ $$$$\:=\:\left[\:\int\:\frac{\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\:\mathrm{dx}}{\mathrm{5}−\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:\:\mathrm{Put},\:\:\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\:=\:\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\mathrm{dx}=\mathrm{2dt} \\ $$$$\:\:\:\left[\:\int\:\:\frac{\mathrm{2dt}}{\mathrm{5}−\mathrm{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{2}\pi} =\:\left[\:\mathrm{2}\int\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} −\left(\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:\:\left[\:\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}\mathrm{log}\:\frac{\:\sqrt{\mathrm{5}}\:\:+{t}}{\:\sqrt{\mathrm{5}}\:−\mathrm{t}}\:\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$=\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{log}\:\frac{\:\:\sqrt{\mathrm{5}}\:+\:\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}}}{\:\sqrt{\mathrm{5}}\:−\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}}}\right)−\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{log}\:\frac{\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\:=\mathrm{0}\://. \\ $$
Commented by john santu last updated on 10/May/20
joss

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *