Menu Close

find-0-cos-x-n-dx-snd-0-sin-x-n-dx-

Tinku Tara 0 Comments
Pin




Question Number 124530 by Bird last updated on 03/Dec/20
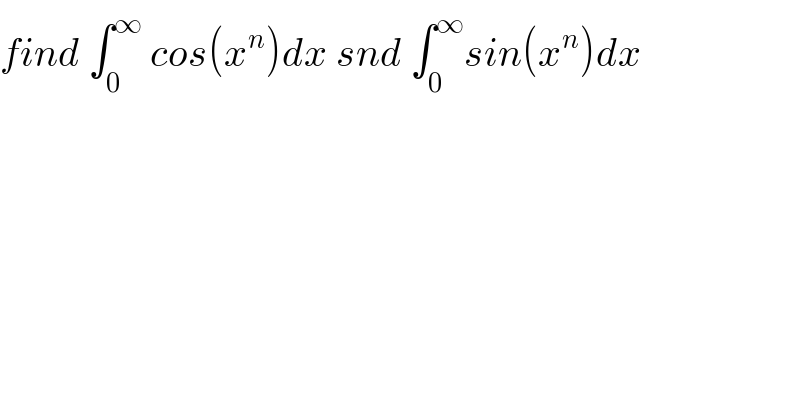
find ∫_0 ^∞ cos(x^n )dx snd ∫_0 ^∞ sin(x^n )dx
$${find}\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{{n}} \right){dx}\:{snd}\:\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{{n}} \right){dx} \\ $$
Commented by Dwaipayan Shikari last updated on 04/Dec/20
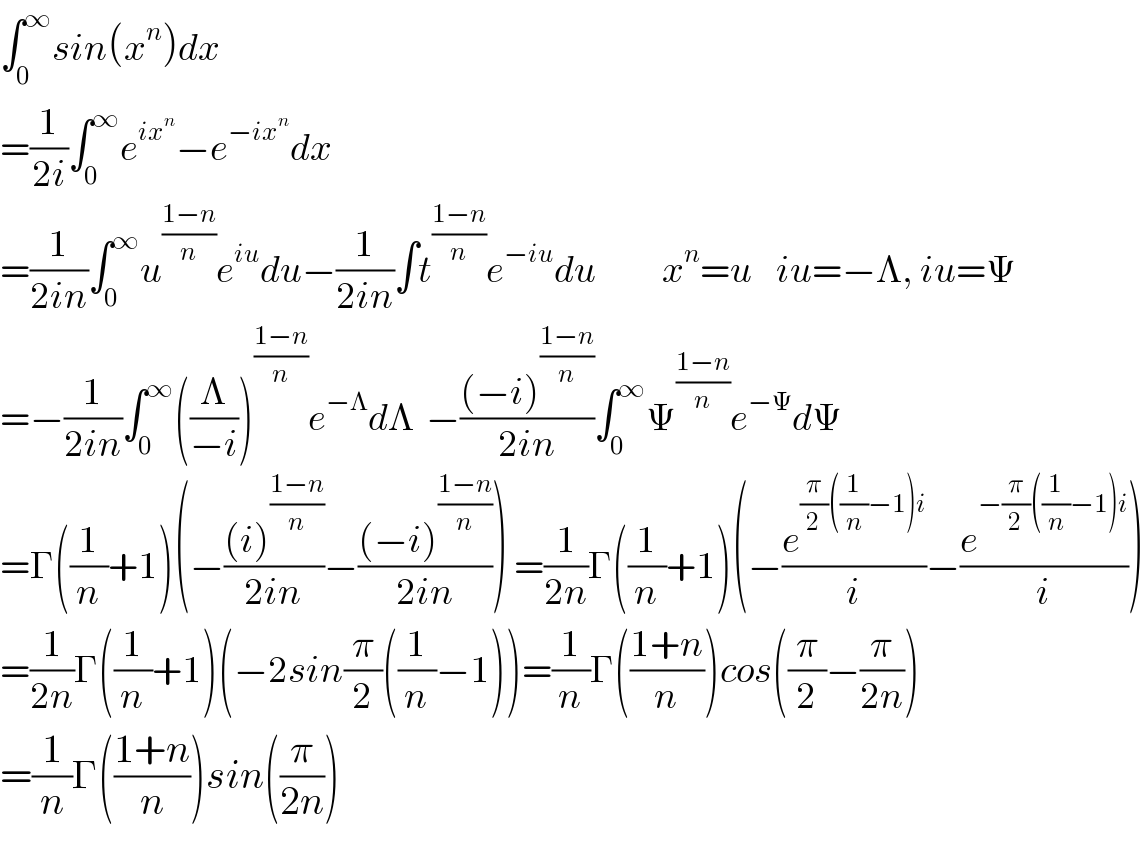
∫_0 ^∞ sin(x^n )dx =(1/(2i))∫_0 ^∞ e^(ix^n ) −e^(−ix^n ) dx =(1/(2in))∫_0 ^∞ u^((1−n)/n) e^(iu) du−(1/(2in))∫t^((1−n)/n) e^(−iu) du x^n =u iu=−Λ, iu=Ψ =−(1/(2in))∫_0 ^∞ ((Λ/(−i)))^((1−n)/n) e^(−Λ) dΛ −(((−i)^((1−n)/n) )/(2in))∫_0 ^∞ Ψ^((1−n)/n) e^(−Ψ) dΨ =Γ((1/n)+1)(−(((i)^((1−n)/n) )/(2in))−(((−i)^((1−n)/n) )/(2in))) =(1/(2n))Γ((1/n)+1)(−(e^((π/2)((1/n)−1)i) /i)−(e^(−(π/2)((1/n)−1)i) /i)) =(1/(2n))Γ((1/n)+1)(−2sin(π/2)((1/n)−1))=(1/n)Γ(((1+n)/n))cos((π/2)−(π/(2n))) =(1/n)Γ(((1+n)/n))sin((π/(2n)))
$$\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{{n}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} {e}^{{ix}^{{n}} } −{e}^{−{ix}^{{n}} } {dx}\:\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{in}}\int_{\mathrm{0}} ^{\infty} {u}^{\frac{\mathrm{1}−{n}}{{n}}} {e}^{{iu}} {du}−\frac{\mathrm{1}}{\mathrm{2}{in}}\int{t}^{\frac{\mathrm{1}−{n}}{{n}}} {e}^{−{iu}} {du}\:\:\:\:\:\:\:\:\:\:\:{x}^{{n}} ={u}\:\:\:\:{iu}=−\Lambda,\:{iu}=\Psi \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{in}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\Lambda}{−{i}}\right)^{\frac{\mathrm{1}−{n}}{{n}}} {e}^{−\Lambda} {d}\Lambda\:\:−\frac{\left(−{i}\right)^{\frac{\mathrm{1}−{n}}{{n}}} }{\mathrm{2}{in}}\int_{\mathrm{0}} ^{\infty} \Psi^{\frac{\mathrm{1}−{n}}{{n}}} {e}^{−\Psi} {d}\Psi \\ $$$$=\Gamma\left(\frac{\mathrm{1}}{{n}}+\mathrm{1}\right)\left(−\frac{\left({i}\right)^{\frac{\mathrm{1}−{n}}{{n}}} }{\mathrm{2}{in}}−\frac{\left(−{i}\right)^{\frac{\mathrm{1}−{n}}{{n}}} }{\mathrm{2}{in}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{n}}\Gamma\left(\frac{\mathrm{1}}{{n}}+\mathrm{1}\right)\left(−\frac{{e}^{\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\mathrm{1}\right){i}} }{{i}}−\frac{{e}^{−\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\mathrm{1}\right){i}} }{{i}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}}\Gamma\left(\frac{\mathrm{1}}{{n}}+\mathrm{1}\right)\left(−\mathrm{2}{sin}\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\mathrm{1}\right)\right)=\frac{\mathrm{1}}{{n}}\Gamma\left(\frac{\mathrm{1}+{n}}{{n}}\right){cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}{n}}\right) \\ $$$$=\frac{\mathrm{1}}{{n}}\Gamma\left(\frac{\mathrm{1}+{n}}{{n}}\right){sin}\left(\frac{\pi}{\mathrm{2}{n}}\right) \\ $$
Answered by mathmax by abdo last updated on 04/Dec/20
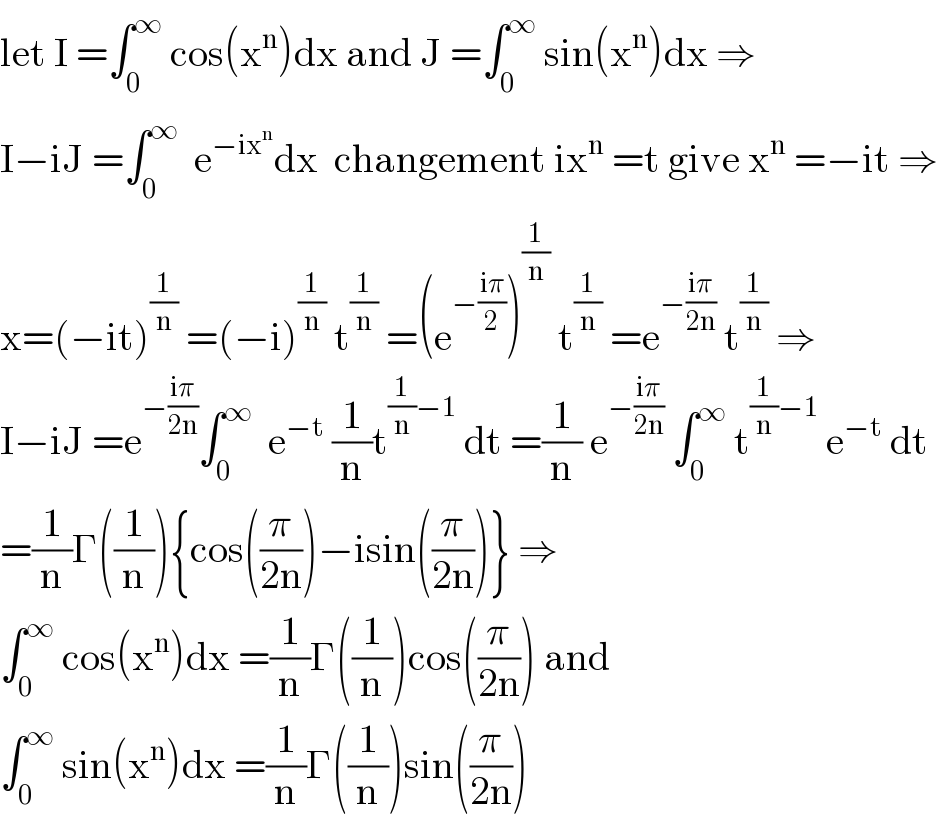
let I =∫_0 ^∞ cos(x^n )dx and J =∫_0 ^∞ sin(x^n )dx ⇒ I−iJ =∫_0 ^∞ e^(−ix^n ) dx changement ix^n =t give x^n =−it ⇒ x=(−it)^(1/n) =(−i)^(1/n) t^(1/n) =(e^(−((iπ)/2)) )^(1/n) t^(1/n) =e^(−((iπ)/(2n))) t^(1/n) ⇒ I−iJ =e^(−((iπ)/(2n))) ∫_0 ^∞ e^(−t) (1/n)t^((1/n)−1) dt =(1/n) e^(−((iπ)/(2n))) ∫_0 ^∞ t^((1/n)−1) e^(−t) dt =(1/n)Γ((1/n)){cos((π/(2n)))−isin((π/(2n)))} ⇒ ∫_0 ^∞ cos(x^n )dx =(1/n)Γ((1/n))cos((π/(2n))) and ∫_0 ^∞ sin(x^n )dx =(1/n)Γ((1/n))sin((π/(2n)))
$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{x}^{\mathrm{n}} \right)\mathrm{dx}\:\mathrm{and}\:\mathrm{J}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\mathrm{x}^{\mathrm{n}} \right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}−\mathrm{iJ}\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{ix}^{\mathrm{n}} } \mathrm{dx}\:\:\mathrm{changement}\:\mathrm{ix}^{\mathrm{n}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}^{\mathrm{n}} \:=−\mathrm{it}\:\Rightarrow \\ $$$$\mathrm{x}=\left(−\mathrm{it}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\left(−\mathrm{i}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2n}}} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow \\ $$$$\mathrm{I}−\mathrm{iJ}\:=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2n}}} \int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{1}}{\mathrm{n}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{n}}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2n}}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\left\{\mathrm{cos}\left(\frac{\pi}{\mathrm{2n}}\right)−\mathrm{isin}\left(\frac{\pi}{\mathrm{2n}}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{x}^{\mathrm{n}} \right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{n}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{2n}}\right)\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\mathrm{x}^{\mathrm{n}} \right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{n}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{2n}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *