Question Number 31100 by abdo imad last updated on 02/Mar/18
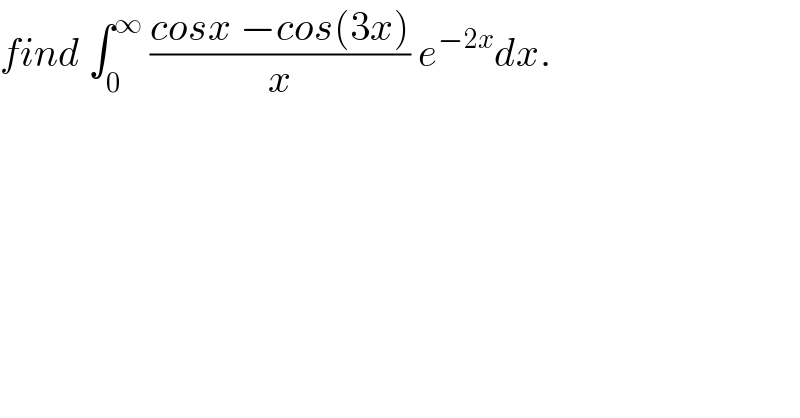
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{cosx}\:−{cos}\left(\mathrm{3}{x}\right)}{{x}}\:{e}^{−\mathrm{2}{x}} {dx}. \\ $$
Commented by abdo imad last updated on 04/Mar/18
![let introduce the function f(t)=∫_0 ^∞ ((cosx −cos(3x))/x)e^(−tx) dx with t>0 after verifying that f is derivable wehave f^′ (t)=−∫_0 ^∞ (cosx −cos(3x))e^(−tx) dx =∫_0 ^∞ cos(3x)e^(−tx) −∫_0 ^∞ cosx e^(−tx) dx let find I_λ =∫_0 ^∞ e^(−tx) cos(λx)dx for λ≥0 I_λ = Re(∫_0 ^∞ e^(−tx) e^(iλx) dx)=Re(∫_0 ^∞ e^((−t+iλ)x) dx)but ∫_0 ^∞ e^((−t+iλ)x) dx=[ (1/(−t+iλ)) e^((−t+iλ)x) ]_(x=0) ^(x→+∞) =((−1)/(−t+iλ)) =(1/(t−iλ))= ((t+iλ)/(t^2 +λ^2 )) ⇒I_λ = (t/(t^2 +λ^2 )) ⇒ f^′ (t)= (t/(t^2 +9)) − (t/(t^2 +1)) ⇒f(t)= ∫( (t/(t^2 +9)) −(t/(t^2 +1)))dt +κ =(1/2)ln(t^2 +9)−(1/2)ln(t^2 +1) +κ=(1/2)ln(((t^2 +9))/(t^2 +1))) +κ but ∃m>0 ∣f(t)∣≤m∫_0 ^∞ e^(−tx) dx=(m/t) →0 for t→∞⇒κ=0and f(t)=(1/2)ln(((t^2 +9)/(t^2 +1))) ⇒ ∫_0 ^∞ ((cosx −cos(3x))/x)e^(−2x) dx=f(2)=(1/2)ln(((13)/5)).](https://www.tinkutara.com/question/Q31235.png)
$${let}\:{introduce}\:{the}\:{function}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{cosx}\:−{cos}\left(\mathrm{3}{x}\right)}{{x}}{e}^{−{tx}} {dx} \\ $$$${with}\:{t}>\mathrm{0}\:{after}\:{verifying}\:{that}\:{f}\:{is}\:{derivable}\:{wehave} \\ $$$${f}^{'} \left({t}\right)=−\int_{\mathrm{0}} ^{\infty} \left({cosx}\:−{cos}\left(\mathrm{3}{x}\right)\right){e}^{−{tx}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {cos}\left(\mathrm{3}{x}\right){e}^{−{tx}} \:−\int_{\mathrm{0}} ^{\infty} {cosx}\:{e}^{−{tx}} {dx}\:{let}\:{find} \\ $$$${I}_{\lambda} =\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} {cos}\left(\lambda{x}\right){dx}\:{for}\:\lambda\geqslant\mathrm{0} \\ $$$${I}_{\lambda} =\:{Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}} \:{e}^{{i}\lambda{x}} {dx}\right)={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{t}+{i}\lambda\right){x}} {dx}\right){but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−{t}+{i}\lambda\right){x}} {dx}=\left[\:\frac{\mathrm{1}}{−{t}+{i}\lambda}\:{e}^{\left(−{t}+{i}\lambda\right){x}} \right]_{{x}=\mathrm{0}} ^{{x}\rightarrow+\infty} =\frac{−\mathrm{1}}{−{t}+{i}\lambda} \\ $$$$=\frac{\mathrm{1}}{{t}−{i}\lambda}=\:\frac{{t}+{i}\lambda}{{t}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:\Rightarrow{I}_{\lambda} =\:\frac{{t}}{{t}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)=\:\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{9}}\:−\:\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{f}\left({t}\right)=\:\int\left(\:\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{9}}\:−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}\:+\kappa \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} +\mathrm{9}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\kappa=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\left.{t}^{\mathrm{2}} \:+\mathrm{9}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}\right)\:+\kappa\:{but} \\ $$$$\exists{m}>\mathrm{0}\:\:\mid{f}\left({t}\right)\mid\leqslant{m}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}} {dx}=\frac{{m}}{{t}}\:\rightarrow\mathrm{0}\:{for}\:{t}\rightarrow\infty\Rightarrow\kappa=\mathrm{0}{and} \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{t}^{\mathrm{2}} \:+\mathrm{9}}{{t}^{\mathrm{2}} +\mathrm{1}}\right)\:\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{cosx}\:−{cos}\left(\mathrm{3}{x}\right)}{{x}}{e}^{−\mathrm{2}{x}} {dx}={f}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{13}}{\mathrm{5}}\right). \\ $$
