Question Number 32359 by prof Abdo imad last updated on 23/Mar/18
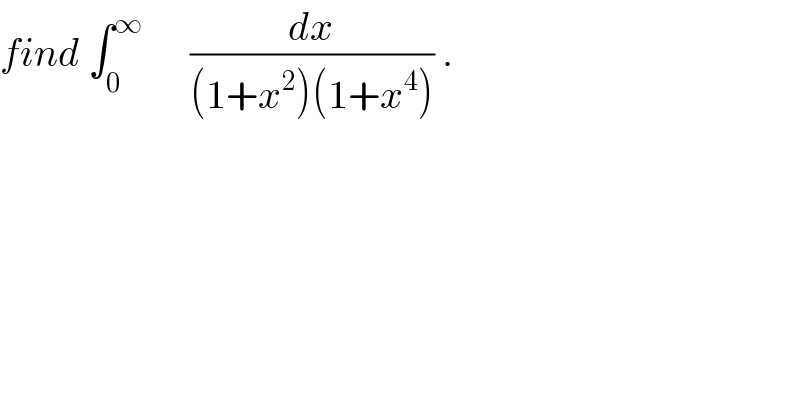
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}\:. \\ $$
Commented by prof Abdo imad last updated on 03/Apr/18
![ch.x=(1/t) give I = ∫_0 ^∞ (1/((1+(1/t^2 ))(1+(1/t^4 )))) (dt/t^2 ) = ∫_0 ^∞ ((t^4 )/((t^2 +1)(1+t^4 ))) dt ⇒ 2I = ∫_0 ^∞ (dt/((1+t^2 )(1+t^4 ))) + ∫_0 ^∞ (t^4 /((1+t^2 )(1+t^4 )))dt = ∫_0 ^∞ (dt/(1+t^2 )) =[arctant]_0 ^∞ = (π/2) ⇒ I =(π/4) .](https://www.tinkutara.com/question/Q32846.png)
$${ch}.{x}=\frac{\mathrm{1}}{{t}}\:{give}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{4}} }\right)}\:\frac{{dt}}{{t}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{t}^{\mathrm{4}} \:\:\:\:\:}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\:{dt}\:\:\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\:+\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\mathrm{4}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\left[{arctant}\right]_{\mathrm{0}} ^{\infty} \:=\:\frac{\pi}{\mathrm{2}}\:\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{4}}\:. \\ $$
