Question Number 123674 by mathmax by abdo last updated on 27/Nov/20
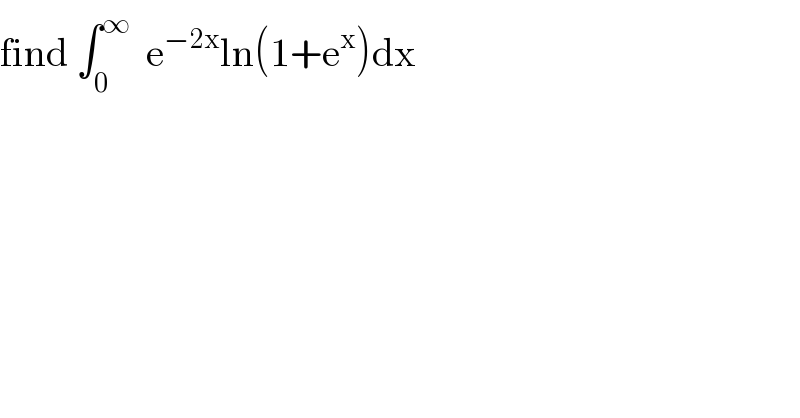
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{2x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 27/Nov/20
![∫_0 ^∞ e^(−2x) log(1+e^x )dx =∫_1 ^∞ ((log(1+t))/t^3 ) dt e^x =t =[((log(t+1))/(−2t^2 ))]_1 ^∞ +∫_1 ^∞ (1/(2t^2 (t+1)))dt =((log2)/2)+∫_1 ^∞ (1/(2t^2 ))−(1/(2t))+(1/(2(t+1)))dt =((log2)/2)+(1/2)+[(1/2)log(((t+1)/t))]_1 ^∞ =(1/2)](https://www.tinkutara.com/question/Q123684.png)
$$\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} {log}\left(\mathrm{1}+{e}^{{x}} \right){dx} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{log}\left(\mathrm{1}+{t}\right)}{{t}^{\mathrm{3}} }\:{dt}\:\:\:\:\:\:{e}^{{x}} ={t} \\ $$$$=\left[\frac{{log}\left({t}+\mathrm{1}\right)}{−\mathrm{2}{t}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\infty} +\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)}{dt} \\ $$$$=\frac{{log}\mathrm{2}}{\mathrm{2}}+\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}{t}}+\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}{dt} \\ $$$$=\frac{{log}\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\left[\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{{t}+\mathrm{1}}{{t}}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 28/Nov/20
![I =∫_0 ^∞ e^(−2x) ln(1+e^x )dx changement e^x =t give I =∫_1 ^∞ t^(−2) ln(1+t)(dt/t) =∫_1 ^∞ t^(−3) ln(1+t)dt =_(by parts) [−(1/2)t^(−2) ln(1+t)]_1 ^∞ +(1/2)∫_1 ^∞ t^(−2) (1/(1+t))dt =((ln(2))/2) +(1/2)∫_1 ^∞ (dt/(t^2 (t+1))) let decompose F(t)=(1/(t^2 (t+1))) F(t)=(a/t)+(b/t^2 ) +(c/(t+1)) b=1 , c=1 ⇒F(t) =(a/t)+(1/t^2 ) +(1/(t+1)) lim_(t→+∞) tF(t)=0 =a+c ⇒a=−1 ⇒F(t)=−(1/t)+(1/t^2 )+(1/(t+1)) ⇒∫_1 ^∞ F(t)dt =∫_1 ^∞ ((1/(t+1))−(1/t))dt +[−(1/t)]_1 ^∞ =[ln∣((t+1)/t)∣]_1 ^∞ +1 =−ln2 +1 ⇒ I =((ln(2))/2)−((ln(2))/2)+(1/2) ⇒ I =(1/2)](https://www.tinkutara.com/question/Q123760.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{1}} ^{\infty} \:\mathrm{t}^{−\mathrm{2}} \mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)\frac{\mathrm{dt}}{\mathrm{t}}\:=\int_{\mathrm{1}} ^{\infty} \:\mathrm{t}^{−\mathrm{3}} \mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)\mathrm{dt} \\ $$$$=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\:\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}^{−\mathrm{2}} \mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)\right]_{\mathrm{1}} ^{\infty} \:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \:\mathrm{t}^{−\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}}{\mathrm{t}}+\frac{\mathrm{b}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{t}+\mathrm{1}} \\ $$$$\mathrm{b}=\mathrm{1}\:\:\:,\:\mathrm{c}=\mathrm{1}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{a}}{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}\:=\mathrm{a}+\mathrm{c}\:\Rightarrow\mathrm{a}=−\mathrm{1}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=−\frac{\mathrm{1}}{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{1}} ^{\infty} \:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\int_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}}\right)\mathrm{dt}\:+\left[−\frac{\mathrm{1}}{\mathrm{t}}\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\left[\mathrm{ln}\mid\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}}\mid\right]_{\mathrm{1}} ^{\infty} +\mathrm{1}\:=−\mathrm{ln2}\:+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
