Menu Close

find-0-ln-1-ix-x-3-8-dx-

Tinku Tara 0 Comments
Pin




Question Number 40580 by maxmathsup by imad last updated on 24/Jul/18
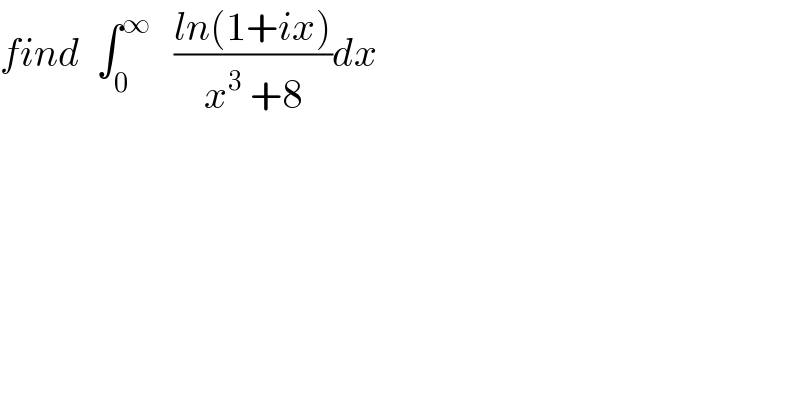
find ∫_0 ^∞ ((ln(1+ix))/(x^3 +8))dx
$${find}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left(\mathrm{1}+{ix}\right)}{{x}^{\mathrm{3}} \:+\mathrm{8}}{dx} \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 28/Jul/18
we have ∣1+ix∣=(√(1+x^2 ))⇒ 1+ix=(√(1+x^2 ))((1/( (√(1+x^2 )))) +i(x/( (√(1+x^2 )))))=r e^(iθ) ⇒ r=(√(1+x^2 )) and tanθ =x ⇒θ=arctan(x) ⇒ ln(1+ix)=ln(r)+iθ =(1/2)ln(1+x^2 ) +i arctanx I = (1/2) ∫_0 ^∞ ((ln(1+x^2 ))/(x^3 +8))dx +i ∫_0 ^∞ ((arctanx)/(x^3 +8))dx let f(t) =∫_0 ^∞ ((ln(1+x^2 t))/(x^3 +8))dx we have f^′ (t) =∫_0 ^∞ (x^2 /((1+tx^2 )(x^8 +3)))dx =(1/t)∫_0 ^∞ ((tx^2 +1−1)/((1+tx^2 )(x^3 +8)))dx =(1/t)∫_0 ^∞ (dx/(x^3 +8)) −(1/t)∫_0 ^∞ (dx/((tx^2 +1)(x^3 +8)))let decompose F(x)=(1/(x^3 +8)) =(1/((x+2)(x^2 −2x+4))) =(a/(x+2)) +((bx+c)/(x^2 −2x+4)) a=lim_(x→−2) (x+2)F(x)= (1/(12)) lim_(x→+∞) xF(x)=0=a+b ⇒b=−(1/(12)) F(x)=(1/(12(x+2))) +((−(1/(12))x +c)/(x^2 −2x+4)) F(0) =(1/8) = (1/(24)) +(c/4) ⇒1=(1/3) +2c ⇒2c=(2/3) ⇒ c=(1/3) ⇒ F(x)=(1/(12(x+2))) −(1/(12)) ((x −4)/(x^2 −2x+4)) ∫_0 ^∞ F(x)dx =(1/(12)){ ∫_0 ^∞ (dx/(x+2)) −(1/2)∫_0 ^∞ ((2x−2−6)/(x^2 −2x+4))dx} =(1/(12)){ [ln∣((x+2)/( (√(x^2 −2x+4))))∣]_0 ^(+∞) +3 ∫_0 ^∞ (dx/(x^2 −2x+4))} =(1/4) ∫_0 ^∞ (dx/(x^2 −2x+1+3)) =(1/4)∫_0 ^∞ (dx/((x−1)^2 +3)) =_(x−1=(√3)u) (1/4) ∫_(−(1/( (√3)))) ^∞ (((√3)du)/(3(1+u^2 ))) = ((√3)/(12))[arctanu]_(−(1/( (√3)))) ^(+∞) =((√3)/(12))((π/2) +arctan((1/( (√3)))))=((√3)/(12))((π/2) +(π/6))=((√3)/(12)).((2π)/3) =((π(√3))/(18)) = ∫_0 ^∞ (dx/(x^3 +8))
$${we}\:{have}\:\mid\mathrm{1}+{ix}\mid=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\Rightarrow \\ $$$$\mathrm{1}+{ix}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+{i}\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)={r}\:{e}^{{i}\theta} \:\Rightarrow \\ $$$${r}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{and}\:{tan}\theta\:={x}\:\Rightarrow\theta={arctan}\left({x}\right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{ix}\right)={ln}\left({r}\right)+{i}\theta\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:+{i}\:{arctanx} \\ $$$${I}\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{3}} \:+\mathrm{8}}{dx}\:+{i}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctanx}}{{x}^{\mathrm{3}} \:+\mathrm{8}}{dx} \\ $$$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} {t}\right)}{{x}^{\mathrm{3}} \:+\mathrm{8}}{dx}\:{we}\:{have} \\ $$$${f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\left({x}^{\mathrm{8}} \:+\mathrm{3}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\infty} \:\frac{{tx}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\left({x}^{\mathrm{3}} \:+\mathrm{8}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{3}} \:+\mathrm{8}}\:−\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({tx}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{3}} \:+\mathrm{8}\right)}{let} \\ $$$${decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{3}} \:+\mathrm{8}}\:=\frac{\mathrm{1}}{\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}\right)} \\ $$$$=\frac{{a}}{{x}+\mathrm{2}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}} \\ $$$${a}={lim}_{{x}\rightarrow−\mathrm{2}} \:\left({x}+\mathrm{2}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}={a}+{b}\:\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{12}\left({x}+\mathrm{2}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{12}}{x}\:+{c}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}} \\ $$$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{\mathrm{8}}\:=\:\frac{\mathrm{1}}{\mathrm{24}}\:+\frac{{c}}{\mathrm{4}}\:\Rightarrow\mathrm{1}=\frac{\mathrm{1}}{\mathrm{3}}\:+\mathrm{2}{c}\:\Rightarrow\mathrm{2}{c}=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$${c}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{12}\left({x}+\mathrm{2}\right)}\:−\frac{\mathrm{1}}{\mathrm{12}}\:\:\:\frac{{x}\:−\mathrm{4}}{{x}^{\mathrm{2}} \:−\mathrm{2}{x}+\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{12}}\left\{\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}+\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{x}−\mathrm{2}−\mathrm{6}}{{x}^{\mathrm{2}} \:−\mathrm{2}{x}+\mathrm{4}}{dx}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left\{\:\:\left[{ln}\mid\frac{{x}+\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}}}\mid\right]_{\mathrm{0}} ^{+\infty} \:+\mathrm{3}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}+\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}} \\ $$$$=_{{x}−\mathrm{1}=\sqrt{\mathrm{3}}{u}} \:\:\frac{\mathrm{1}}{\mathrm{4}}\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\infty} \:\:\:\frac{\sqrt{\mathrm{3}}{du}}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\left[{arctanu}\right]_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\left(\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\left(\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{6}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}.\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{18}}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{3}} \:+\mathrm{8}} \\ $$
Commented by math khazana by abdo last updated on 28/Jul/18
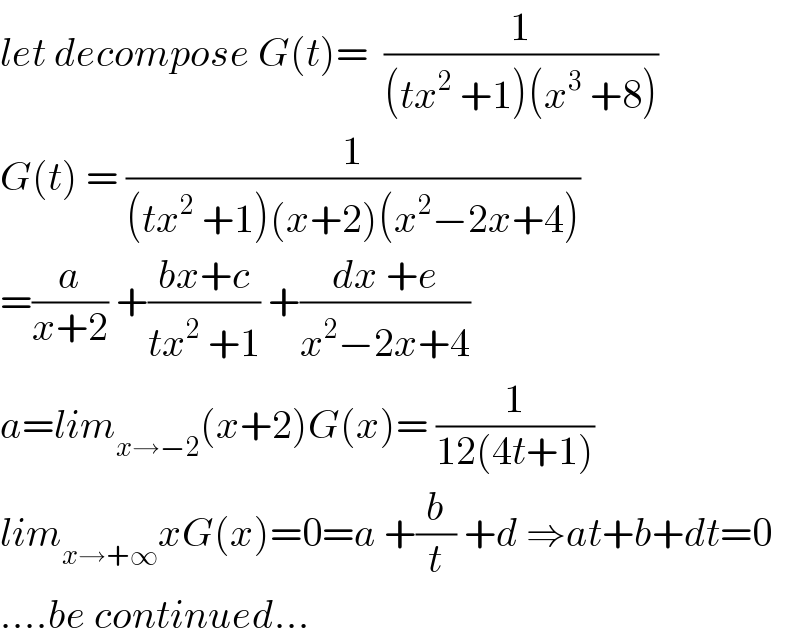
let decompose G(t)= (1/((tx^2 +1)(x^3 +8))) G(t) = (1/((tx^2 +1)(x+2)(x^2 −2x+4))) =(a/(x+2)) +((bx+c)/(tx^2 +1)) +((dx +e)/(x^2 −2x+4)) a=lim_(x→−2) (x+2)G(x)= (1/(12(4t+1))) lim_(x→+∞) xG(x)=0=a +(b/t) +d ⇒at+b+dt=0 ....be continued...
$${let}\:{decompose}\:{G}\left({t}\right)=\:\:\frac{\mathrm{1}}{\left({tx}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{3}} \:+\mathrm{8}\right)} \\ $$$${G}\left({t}\right)\:=\:\frac{\mathrm{1}}{\left({tx}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}\right)} \\ $$$$=\frac{{a}}{{x}+\mathrm{2}}\:+\frac{{bx}+{c}}{{tx}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{dx}\:+{e}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}} \\ $$$${a}={lim}_{{x}\rightarrow−\mathrm{2}} \left({x}+\mathrm{2}\right){G}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{12}\left(\mathrm{4}{t}+\mathrm{1}\right)} \\ $$$${lim}_{{x}\rightarrow+\infty} {xG}\left({x}\right)=\mathrm{0}={a}\:+\frac{{b}}{{t}}\:+{d}\:\Rightarrow{at}+{b}+{dt}=\mathrm{0} \\ $$$$….{be}\:{continued}… \\ $$
Commented by math khazana by abdo last updated on 28/Jul/18
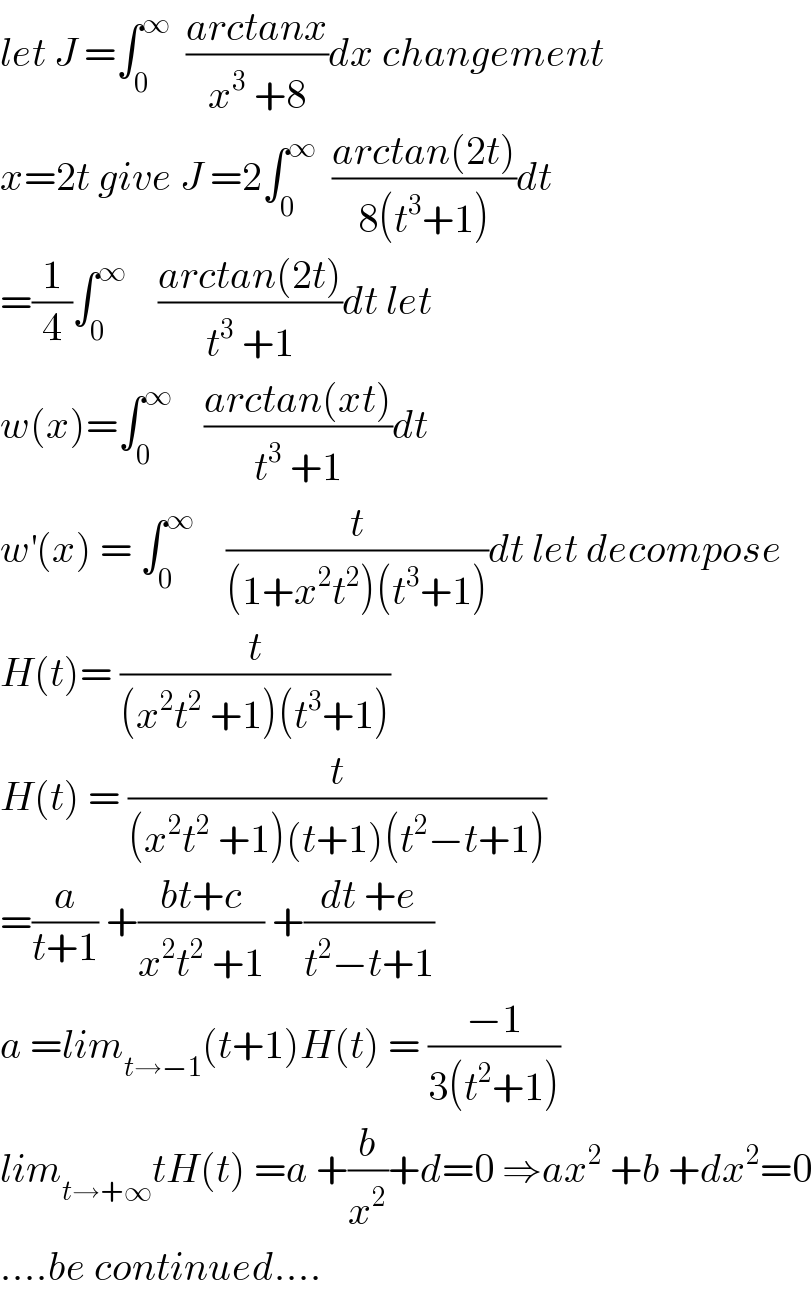
let J =∫_0 ^∞ ((arctanx)/(x^3 +8))dx changement x=2t give J =2∫_0 ^∞ ((arctan(2t))/(8(t^3 +1)))dt =(1/4)∫_0 ^∞ ((arctan(2t))/(t^3 +1))dt let w(x)=∫_0 ^∞ ((arctan(xt))/(t^3 +1))dt w^′ (x) = ∫_0 ^∞ (t/((1+x^2 t^2 )(t^3 +1)))dt let decompose H(t)= (t/((x^2 t^2 +1)(t^3 +1))) H(t) = (t/((x^2 t^2 +1)(t+1)(t^2 −t+1))) =(a/(t+1)) +((bt+c)/(x^2 t^2 +1)) +((dt +e)/(t^2 −t+1)) a =lim_(t→−1) (t+1)H(t) = ((−1)/(3(t^2 +1))) lim_(t→+∞) tH(t) =a +(b/x^2 )+d=0 ⇒ax^2 +b +dx^2 =0 ....be continued....
$${let}\:{J}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctanx}}{{x}^{\mathrm{3}} \:+\mathrm{8}}{dx}\:{changement} \\ $$$${x}=\mathrm{2}{t}\:{give}\:{J}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{2}{t}\right)}{\mathrm{8}\left({t}^{\mathrm{3}} +\mathrm{1}\right)}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{arctan}\left(\mathrm{2}{t}\right)}{{t}^{\mathrm{3}} \:+\mathrm{1}}{dt}\:{let} \\ $$$${w}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{arctan}\left({xt}\right)}{{t}^{\mathrm{3}} \:+\mathrm{1}}{dt} \\ $$$${w}^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{t}}{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)\left({t}^{\mathrm{3}} +\mathrm{1}\right)}{dt}\:{let}\:{decompose} \\ $$$${H}\left({t}\right)=\:\frac{{t}}{\left({x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{3}} +\mathrm{1}\right)} \\ $$$${H}\left({t}\right)\:=\:\frac{{t}}{\left({x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)} \\ $$$$=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{bt}+{c}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{dt}\:+{e}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){H}\left({t}\right)\:=\:\frac{−\mathrm{1}}{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${lim}_{{t}\rightarrow+\infty} {tH}\left({t}\right)\:={a}\:+\frac{{b}}{{x}^{\mathrm{2}} }+{d}=\mathrm{0}\:\Rightarrow{ax}^{\mathrm{2}} \:+{b}\:+{dx}^{\mathrm{2}} =\mathrm{0} \\ $$$$….{be}\:{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *