Question Number 118955 by Bird last updated on 21/Oct/20
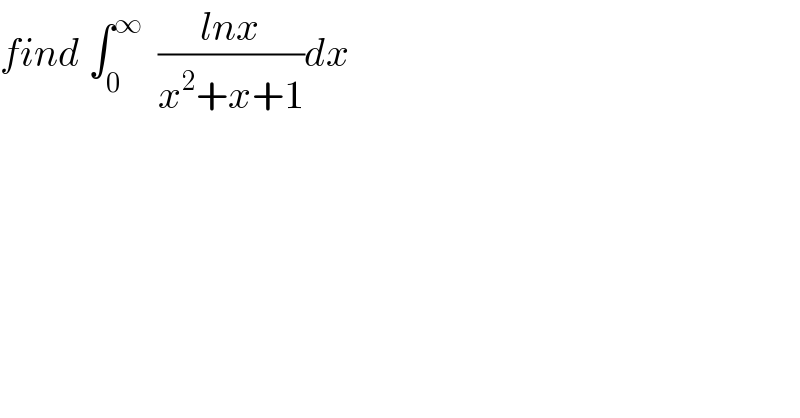
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$
Answered by mnjuly1970 last updated on 21/Oct/20
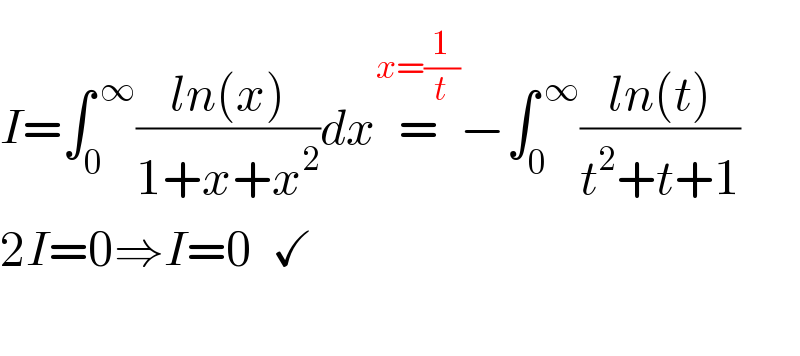
$$ \\ $$$${I}=\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}\overset{{x}=\frac{\mathrm{1}}{{t}}} {=}−\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} +{t}+\mathrm{1}} \\ $$$$\mathrm{2}{I}=\mathrm{0}\Rightarrow{I}=\mathrm{0}\:\:\checkmark \\ $$$$ \\ $$
