Question Number 31501 by abdo imad last updated on 09/Mar/18
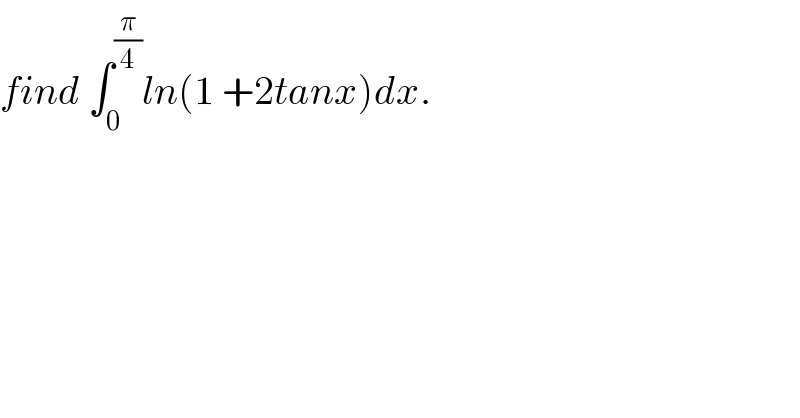
$${find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}\:+\mathrm{2}{tanx}\right){dx}. \\ $$
Commented by abdo imad last updated on 12/Mar/18

$${let}\:{introduce}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\mathrm{1}\:+{ttanx}\right){dx}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{tanx}}{\mathrm{1}+{t}\:{tanx}}{dx}\:=\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{t}\:{tanx}\:+\mathrm{1}−\mathrm{1}}{\mathrm{1}+{t}\:{tanx}}{dx} \\ $$$$=\frac{\pi}{\mathrm{4}{t}}\:−\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dx}}{\mathrm{1}+{t}\:{tanx}}\:{but}\:{we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dx}}{\mathrm{1}+{t}\:{tanx}}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{cosx}}{{cosx}\:+{t}\:{sinx}}{dx}\:\:{let}\:{use}\:{thech}. \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)={u}\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{cosx}}{{cosx}\:+{t}\:{sinx}}{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\frac{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\:+{t}\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}−{u}^{\mathrm{2}} \:+\mathrm{2}{tu}\right)}{du} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\frac{{u}^{\mathrm{2}} \:−\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\:{u}^{\mathrm{2}\:} −\mathrm{2}{tu}\:−\mathrm{1}\right)}{du}\:{let}\:{decompose} \\ $$$${F}\left({u}\right)=\frac{{u}^{\mathrm{2}} \:−\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:−\mathrm{2}{tu}\:−\mathrm{1}\right)}\:{roots}\:{of}\:{u}^{\mathrm{2}} \:−\mathrm{2}{tu}\:−\mathrm{1}=\mathrm{0} \\ $$$$\Delta^{'} \:={t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow\:{u}_{\mathrm{1}} ={t}\:+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} \:}\:\:{and}\:\:{u}_{\mathrm{2}} ={t}−\sqrt{\mathrm{1}+{t}^{\mathrm{2}} \:\:}\:\Rightarrow \\ $$$${F}\left({u}\right)=\:\frac{{a}}{{u}\:−{u}_{\mathrm{1}} }\:+\:\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\:\frac{{cu}\:+{d}}{\mathrm{1}+{u}^{\mathrm{2}} }\:….{be}\:{continued}… \\ $$
