Menu Close

find-0-pi-4-ln-1-tanx-dx-

Tinku Tara 0 Comments
Pin




Question Number 29451 by prof Abdo imad last updated on 08/Feb/18
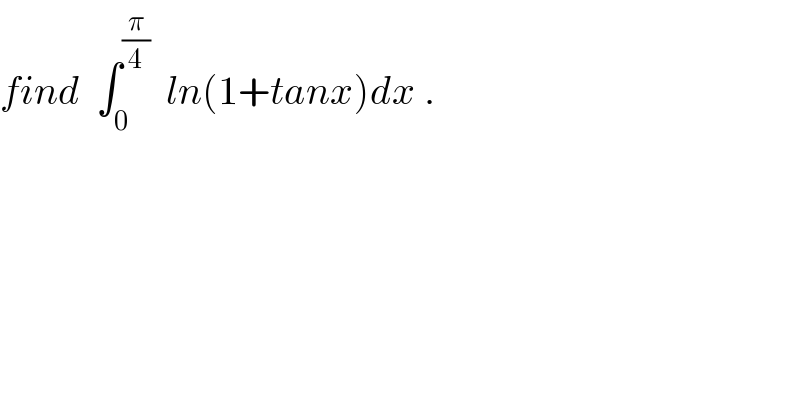
find ∫_0 ^(π/4) ln(1+tanx)dx .
$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{ln}\left(\mathrm{1}+{tanx}\right){dx}\:. \\ $$
Commented by prof Abdo imad last updated on 28/Feb/18
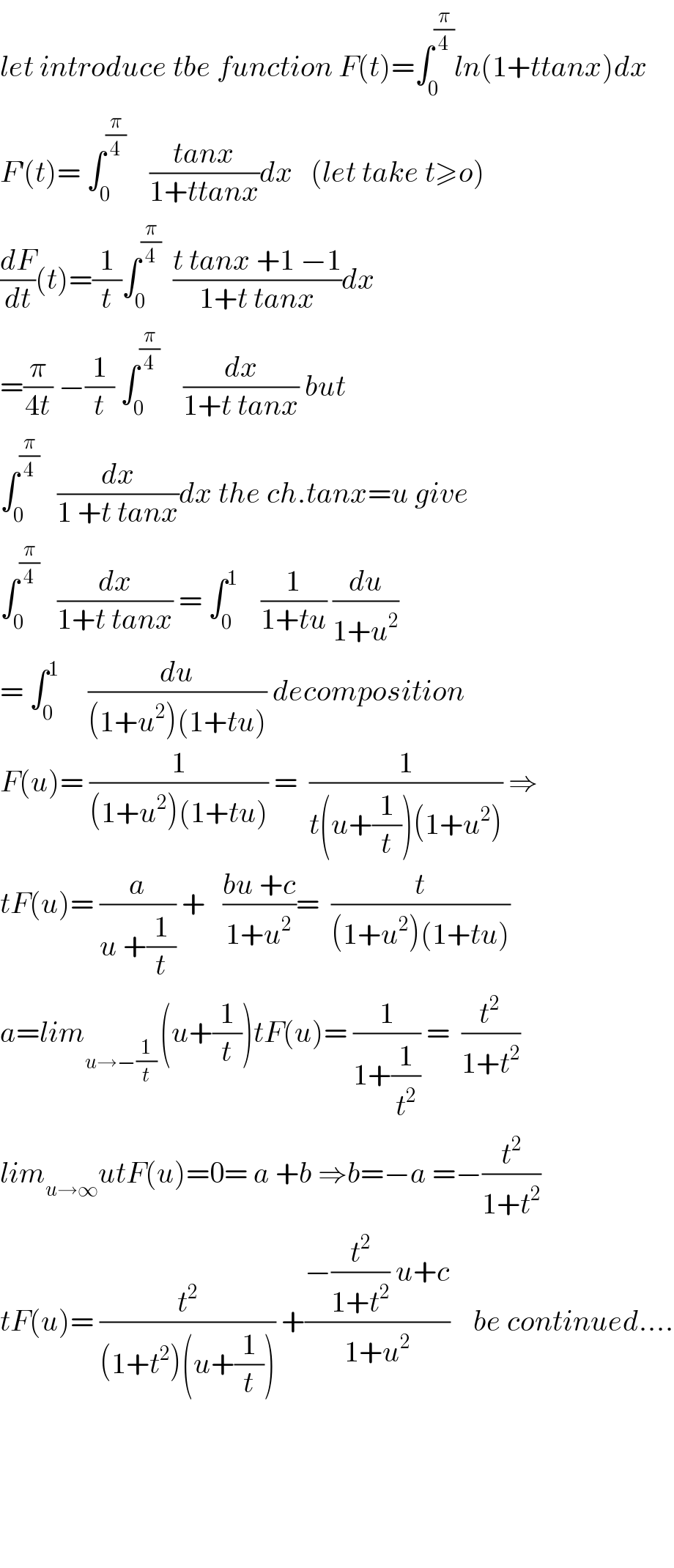
let introduce tbe function F(t)=∫_0 ^(π/4) ln(1+ttanx)dx F^′ (t)= ∫_0 ^(π/4) ((tanx)/(1+ttanx))dx (let take t≥o) (dF/dt)(t)=(1/t)∫_0 ^(π/4) ((t tanx +1 −1)/(1+t tanx))dx =(π/(4t)) −(1/t) ∫_0 ^(π/4) (dx/(1+t tanx)) but ∫_0 ^(π/4) (dx/(1 +t tanx))dx the ch.tanx=u give ∫_0 ^(π/4) (dx/(1+t tanx)) = ∫_0 ^1 (1/(1+tu)) (du/(1+u^2 )) = ∫_0 ^1 (du/((1+u^2 )(1+tu))) decomposition F(u)= (1/((1+u^2 )(1+tu))) = (1/(t(u+(1/t))(1+u^2 ))) ⇒ tF(u)= (a/(u +(1/t))) + ((bu +c)/(1+u^2 ))= (t/((1+u^2 )(1+tu))) a=lim_(u→−(1/t) ) (u+(1/t))tF(u)= (1/(1+(1/t^2 ))) = (t^(2 ) /(1+t^2 )) lim_(u→∞) utF(u)=0= a +b ⇒b=−a =−(t^2 /(1+t^2 )) tF(u)= (t^2 /((1+t^2 )(u+(1/t)))) +((−(t^2 /(1+t^2 )) u+c)/(1+u^2 )) be continued....
$${let}\:{introduce}\:{tbe}\:{function}\:{F}\left({t}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{ttanx}\right){dx} \\ $$$${F}^{'} \left({t}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{tanx}}{\mathrm{1}+{ttanx}}{dx}\:\:\:\left({let}\:{take}\:{t}\geqslant{o}\right) \\ $$$$\frac{{dF}}{{dt}}\left({t}\right)=\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{t}\:{tanx}\:+\mathrm{1}\:−\mathrm{1}}{\mathrm{1}+{t}\:{tanx}}{dx} \\ $$$$=\frac{\pi}{\mathrm{4}{t}}\:−\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dx}}{\mathrm{1}+{t}\:{tanx}}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dx}}{\mathrm{1}\:+{t}\:{tanx}}{dx}\:{the}\:{ch}.{tanx}={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dx}}{\mathrm{1}+{t}\:{tanx}}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{tu}}\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{tu}\right)}\:{decomposition} \\ $$$${F}\left({u}\right)=\:\frac{\mathrm{1}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{tu}\right)}\:=\:\:\frac{\mathrm{1}}{{t}\left({u}+\frac{\mathrm{1}}{{t}}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$${tF}\left({u}\right)=\:\frac{{a}}{{u}\:+\frac{\mathrm{1}}{{t}}}\:+\:\:\:\frac{{bu}\:+{c}}{\mathrm{1}+{u}^{\mathrm{2}} }=\:\:\frac{{t}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{tu}\right)} \\ $$$${a}={lim}_{{u}\rightarrow−\frac{\mathrm{1}}{{t}}\:} \left({u}+\frac{\mathrm{1}}{{t}}\right){tF}\left({u}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\:=\:\:\frac{{t}^{\mathrm{2}\:} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow\infty} {utF}\left({u}\right)=\mathrm{0}=\:{a}\:+{b}\:\Rightarrow{b}=−{a}\:=−\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${tF}\left({u}\right)=\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({u}+\frac{\mathrm{1}}{{t}}\right)}\:+\frac{−\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{u}+{c}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\:\:\:{be}\:{continued}…. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *