Question Number 40658 by math khazana by abdo last updated on 25/Jul/18
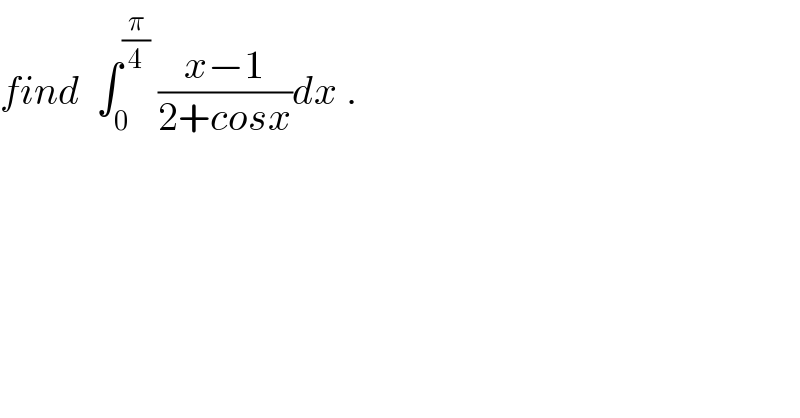
$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{x}−\mathrm{1}}{\mathrm{2}+{cosx}}{dx}\:. \\ $$
Commented by math khazana by abdo last updated on 26/Jul/18
![let I = ∫_0 ^(π/4) ((x−1)/(2+cosx))dx changement tan((x/2))=t give I = ∫_0 ^((√2)−1) ((2arctant−1)/(2+((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = 2 ∫_0 ^((√2)−1) ((2arctant −1)/(2+2t^2 +1−t^2 ))dt = 2 ∫_0 ^((√2)−1) ((2arctan(t)−1)/(3+t^2 ))dt =4 ∫_0 ^((√2)−1) ((arctan(t))/(3+t^2 ))dt −2 ∫_0 ^((√2)−1) (dt/(3+t^2 )) but ∫_0 ^((√2)−1) (dt/(3+t^2 )) =_(t=(√3)u) ∫_0 ^(((√2)−1)/( (√3))) (((√3)du)/(3(1+u^2 ))) =((√3)/3) [ arctan(u)]_0 ^(((√2)−1)/( (√3))) =((√3)/3) arctan((((√2)−1)/( (√3)))). let f(x)= ∫_0 ^((√2)−1) ((arctan(xt))/(3 +t^2 )) dt we have f^′ (x)= ∫_0 ^((√2)−1) (t/((3+t^2 )(1+x^2 t^2 )))dt let decompose F(t) = (t/((3+t^2 )(1+x^2 t^2 ))) F(t) = ((at +b)/(t^2 +3)) + ((ct +d)/(x^2 t^2 +1)) F(−t)=−F(t)⇒ ((−at +b)/(t^2 +3)) +((−ct +d)/(x^2 t^2 +1)) =((−at−b)/(t^2 +3)) +((−ct−d)/(x^2 t^2 +1)) ⇒b=d=0 ⇒ F(t) = ((at)/(t^2 +3)) +((ct)/(x^2 t^2 +1)) lim_(t→+∞) tF(t) =0= a +(c/x^2 ) ⇒ax^2 +c =0 ⇒c=−ax^2 ⇒F(x) = ((at)/(t^2 +3)) −((ax^2 t)/(x^2 t^2 +1)) F(1) = (1/(4(1+x^2 ))) = (a/4) −((ax^2 )/(x^2 +1)) ⇒ 1=((4(1+x^2 )a)/4) −4(1+x^2 ) ((ax^2 )/(x^2 +1)) ⇒ 1=(1+x^2 )a −4ax^2 =(1+x^2 −4x^2 )a=(1−3x^2 )a ⇒a =(1/(1−3x^2 )) ⇒ F(x) = (1/(1−3x^2 )){ (t/(t^2 +3)) −((x^2 t)/(x^2 t^2 +1))}⇒ ∫_0 ^((√2)−1) F(t)dt =(1/(1−3x^2 )){ ∫_0 ^((√2)−1) ((tdt)/(t^2 +3)) −∫_0 ^((√2)−1) ((x^2 t)/(x^2 t^2 +1))dt} but ∫_0 ^((√2)−1) ((tdt)/(t^2 +3)) =(1/2)[ln(t^2 +3)]_0 ^((√2)−1) =(1/2){ln( ((√2)−1)^2 +3)−ln(3)} ∫_0 ^((√2)−1) ((x^2 t)/(x^2 t^2 +1))dt =[(1/2)ln(x^2 t^2 +1)]_(t=0) ^(t=(√2)−1) =(1/2){ ln(x^2 ((√2)−1)^2 +1) ∫_0 ^((√2)−1) F(t)dt = (1/(1−3x^2 )){ (1/2)ln(((√2)−1)^2 +3)−(1/2)ln(3)} −(1/2){ ln(((√2)−1)^2 x^2 +1)....be continued...](https://www.tinkutara.com/question/Q40730.png)
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{x}−\mathrm{1}}{\mathrm{2}+{cosx}}{dx}\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t} \\ $$$${give}\:{I}\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{\mathrm{2}{arctant}−\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{2}{arctant}\:−\mathrm{1}}{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$=\:\mathrm{2}\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{arctan}\left({t}\right)−\mathrm{1}}{\mathrm{3}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{{arctan}\left({t}\right)}{\mathrm{3}+{t}^{\mathrm{2}} }{dt}\:−\mathrm{2}\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{3}+{t}^{\mathrm{2}} }\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{{dt}}{\mathrm{3}+{t}^{\mathrm{2}} }\:=_{{t}=\sqrt{\mathrm{3}}{u}} \:\:\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\frac{\sqrt{\mathrm{3}}{du}}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\:\left[\:{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right). \\ $$$${let}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{{arctan}\left({xt}\right)}{\mathrm{3}\:+{t}^{\mathrm{2}} }\:{dt} \\ $$$${we}\:{have}\:{f}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\:\frac{{t}}{\left(\mathrm{3}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}{dt} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\:\frac{{t}}{\left(\mathrm{3}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)} \\ $$$${F}\left({t}\right)\:=\:\frac{{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:+\:\frac{{ct}\:+{d}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(−{t}\right)=−{F}\left({t}\right)\Rightarrow\:\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:+\frac{−{ct}\:+{d}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{−{at}−{b}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:+\frac{−{ct}−{d}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{b}={d}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:\frac{{at}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:+\frac{{ct}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)\:=\mathrm{0}=\:{a}\:+\frac{{c}}{{x}^{\mathrm{2}} }\:\Rightarrow{ax}^{\mathrm{2}} \:+{c}\:=\mathrm{0}\:\Rightarrow{c}=−{ax}^{\mathrm{2}} \\ $$$$\Rightarrow{F}\left({x}\right)\:=\:\frac{{at}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:−\frac{{ax}^{\mathrm{2}} {t}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=\:\frac{{a}}{\mathrm{4}}\:−\frac{{ax}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{1}=\frac{\mathrm{4}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){a}}{\mathrm{4}}\:−\mathrm{4}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\frac{{ax}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{1}=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){a}\:−\mathrm{4}{ax}^{\mathrm{2}} \:=\left(\mathrm{1}+{x}^{\mathrm{2}} \:−\mathrm{4}{x}^{\mathrm{2}} \right){a}=\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right){a} \\ $$$$\Rightarrow{a}\:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\left\{\:\:\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:−\frac{{x}^{\mathrm{2}} {t}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}}\right\}\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} {F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\left\{\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{{tdt}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:−\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{{x}^{\mathrm{2}} {t}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\right\} \\ $$$${but}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{{tdt}}{{t}^{\mathrm{2}} \:+\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left({t}^{\mathrm{2}} \:+\mathrm{3}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\right)−{ln}\left(\mathrm{3}\right)\right\} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{{x}^{\mathrm{2}} {t}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{1}\right)\right]_{{t}=\mathrm{0}} ^{{t}=\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{ln}\left({x}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)\right. \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} {F}\left({t}\right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\left\{\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\right\} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{ln}\left(\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{1}\right)….{be}\:{continued}…\right. \\ $$$$ \\ $$
