Question Number 62001 by maxmathsup by imad last updated on 13/Jun/19
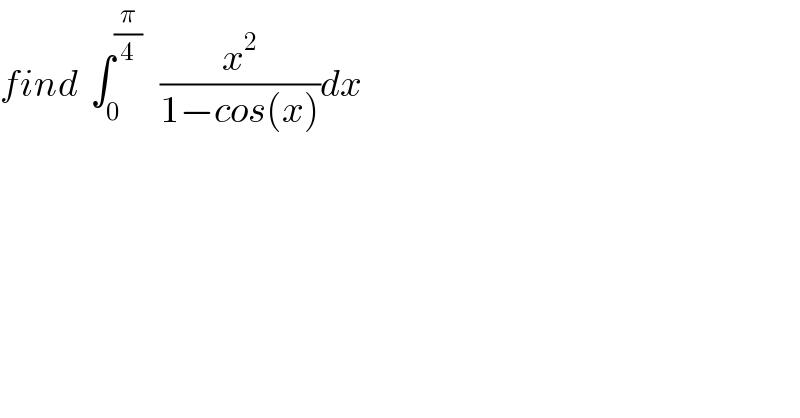
$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{cos}\left({x}\right)}{dx}\: \\ $$
Commented by maxmathsup by imad last updated on 14/Jun/19
![approximate value let I =∫_0 ^(π/4) (x^2 /(1−cosx))dx we have cosx =Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n)!)) (with radius R=∞) ⇒cosx =1−(x^2 /2) +(x^4 /(4!))−... ⇒1−(x^2 /2) ≤cosx≤1−(x^2 /2) +(x^4 /(4!)) ⇒ −1+(x^2 /2)−(x^4 /(4!)) ≤−cosx ≤−1+(x^2 /2) ⇒(x^2 /2) −(x^4 /(4!)) ≤ 1−cosx ≤(x^2 /2) ⇒ (2/x^2 ) ≤(1/(1−cosx)) ≤ (1/((x^2 /2)−(x^4 /(4!)))) ⇒2 ≤ (x^2 /(1−cosx)) ≤ (1/((1/2)−(x^2 /(4!)))) ⇒ ∫_0 ^(π/4) 2dx ≤ ∫_0 ^(π/4) (x^2 /(1−cosx))dx ≤ ∫_0 ^(π/4) (dx/((1/2)−(x^2 /(4!)))) ⇒(π/2) ≤ I ≤2.4! ∫_0 ^(π/4) (dx/(4!−2x^2 )) ∫_0 ^(π/4) (dx/(4!−2x^2 )) =∫_0 ^(π/4) (dx/(24−2x^2 )) =(1/2) ∫_0 ^(π/4) (dx/(12−x^2 )) =(1/2) ∫_0 ^(π/4) (dx/((2(√3)−x)(2(√3)+x))) =(1/2) (1/(4(√3)))∫_0 ^(π/4) { (1/(2(√3)−x)) +(1/(2(√3) +x))}dx = (1/(8(√3)))[ln∣((2(√3)+x)/(2(√3)−x))∣]_0 ^(π/4) =(1/(8(√3))) ln∣((2(√3)+(π/4))/(2(√3)−(π/4)))∣ =(1/(8(√3)))ln∣((8(√3)+π)/(8(√3)−π))∣ ⇒ (π/2) ≤ I ≤ ((2.24)/(8(√3)))ln∣((8(√3)+π)/(8(√3)−π))∣ ⇒ (π/2) ≤ I≤ (6/( (√3)))ln∣((8(√3)+π)/(8(√3)−π))∣ let v_0 =(π/4) +(√3)ln(((8(√3)+π)/(8(√3)−π))) v_0 is a approximate value for this integral .](https://www.tinkutara.com/question/Q62025.png)
$${approximate}\:{value}\:\:{let}\:\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{cosx}}{dx}\:\:\:{we}\:{have}\: \\ $$$${cosx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\:\left({with}\:{radius}\:{R}=\infty\right)\:\Rightarrow{cosx}\:=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−…\:\Rightarrow\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\leqslant{cosx}\leqslant\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}\:\Rightarrow \\ $$$$−\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}\:\leqslant−{cosx}\:\leqslant−\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}\:\leqslant\:\mathrm{1}−{cosx}\:\leqslant\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\: \\ $$$$\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\:\leqslant\frac{\mathrm{1}}{\mathrm{1}−{cosx}}\:\leqslant\:\frac{\mathrm{1}}{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}}\:\Rightarrow\mathrm{2}\:\leqslant\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{cosx}}\:\leqslant\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}!}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\mathrm{2}{dx}\:\leqslant\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{cosx}}{dx}\:\leqslant\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dx}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}!}}\:\Rightarrow\frac{\pi}{\mathrm{2}}\:\leqslant\:{I}\:\leqslant\mathrm{2}.\mathrm{4}!\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dx}}{\mathrm{4}!−\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dx}}{\mathrm{4}!−\mathrm{2}{x}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dx}}{\mathrm{24}−\mathrm{2}{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dx}}{\mathrm{12}−{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dx}}{\left(\mathrm{2}\sqrt{\mathrm{3}}−{x}\right)\left(\mathrm{2}\sqrt{\mathrm{3}}+{x}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left\{\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}−{x}}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}\:+{x}}\right\}{dx}\:=\:\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{3}}}\left[{ln}\mid\frac{\mathrm{2}\sqrt{\mathrm{3}}+{x}}{\mathrm{2}\sqrt{\mathrm{3}}−{x}}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{3}}}\:{ln}\mid\frac{\mathrm{2}\sqrt{\mathrm{3}}+\frac{\pi}{\mathrm{4}}}{\mathrm{2}\sqrt{\mathrm{3}}−\frac{\pi}{\mathrm{4}}}\mid\:=\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{3}}}{ln}\mid\frac{\mathrm{8}\sqrt{\mathrm{3}}+\pi}{\mathrm{8}\sqrt{\mathrm{3}}−\pi}\mid\:\Rightarrow\:\frac{\pi}{\mathrm{2}}\:\leqslant\:{I}\:\leqslant\:\frac{\mathrm{2}.\mathrm{24}}{\mathrm{8}\sqrt{\mathrm{3}}}{ln}\mid\frac{\mathrm{8}\sqrt{\mathrm{3}}+\pi}{\mathrm{8}\sqrt{\mathrm{3}}−\pi}\mid\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}\:\leqslant\:{I}\leqslant\:\:\frac{\mathrm{6}}{\:\sqrt{\mathrm{3}}}{ln}\mid\frac{\mathrm{8}\sqrt{\mathrm{3}}+\pi}{\mathrm{8}\sqrt{\mathrm{3}}−\pi}\mid\:\:{let}\:{v}_{\mathrm{0}} =\frac{\pi}{\mathrm{4}}\:+\sqrt{\mathrm{3}}{ln}\left(\frac{\mathrm{8}\sqrt{\mathrm{3}}+\pi}{\mathrm{8}\sqrt{\mathrm{3}}−\pi}\right) \\ $$$${v}_{\mathrm{0}} {is}\:{a}\:{approximate}\:{value}\:{for}\:{this}\:{integral}\:. \\ $$
