Question Number 29439 by prof Abdo imad last updated on 08/Feb/18
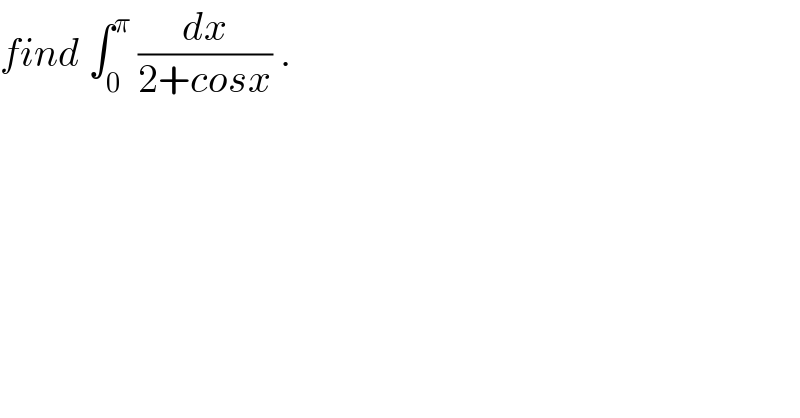
$${find}\:\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{\mathrm{2}+{cosx}}\:. \\ $$
Answered by sma3l2996 last updated on 09/Feb/18
![t=tanx/2⇒dx=((2dt)/(1+t^2 )) ∫_0 ^π (dx/(2+cosx))=∫_0 ^(+∞) (1/(2+((1−t^2 )/(1+t^2 ))))×((2dt)/(1+t^2 )) =2∫_0 ^(+∞) (dt/(3+t^2 ))=(2/3)∫_0 ^(+∞) (dt/(1+((t/( (√3))))^2 )) (√3)u=t⇒dt=(√3)du ∫_0 ^(π/2) (dx/(2+cosx))=((2(√3))/3)∫_0 ^(+∞) (du/(1+u^2 ))=((2(√3))/3)[arctanu]_0 ^(+∞) =((2(√3))/3)×(π/2)=(((√3)π)/3)](https://www.tinkutara.com/question/Q29467.png)
$${t}={tanx}/\mathrm{2}\Rightarrow{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\mathrm{2}+{cosx}}=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{{dt}}{\mathrm{3}+{t}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{+\infty} \frac{{dt}}{\mathrm{1}+\left(\frac{{t}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{3}}{u}={t}\Rightarrow{dt}=\sqrt{\mathrm{3}}{du} \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{dx}}{\mathrm{2}+{cosx}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int_{\mathrm{0}} ^{+\infty} \frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[{arctanu}\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}×\frac{\pi}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}\pi}{\mathrm{3}} \\ $$
