Question Number 61803 by maxmathsup by imad last updated on 09/Jun/19
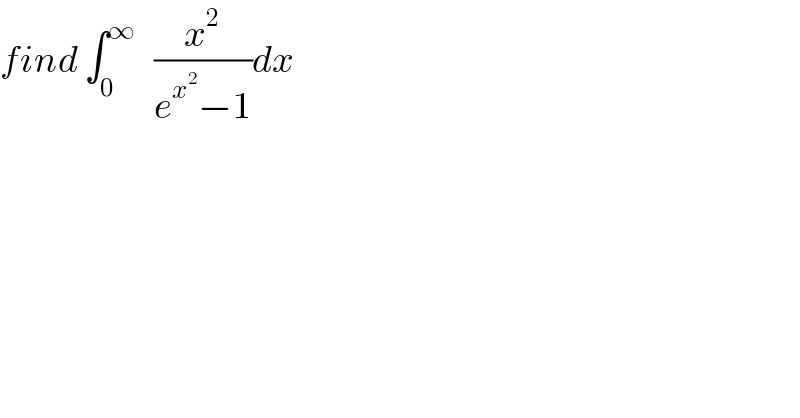
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{2}} }{{e}^{{x}^{\mathrm{2}} } −\mathrm{1}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 09/Jun/19
![let I = ∫_0 ^∞ (x^2 /(e^x^2 −1)) dx ⇒ I =∫_0 ^∞ ((x^2 e^(−x^2 ) )/(1−e^(−x^2 ) )) dx =∫_0 ^∞ x^2 e^(−x^2 ) (Σ_(n=0) ^∞ e^(−nx^2 ) dx) =Σ_(n=0) ^∞ ∫_0 ^∞ x^2 e^(−(n+1)x^2 ) dx =Σ_(n=0) ^∞ W_n with W_n =∫_0 ^∞ x^2 e^(−(n+1)x^2 ) =∫_0 ^∞ x (xe^(−(n+1)x^2 ) )dx by parts u =x and v^′ =x e^(−(n+1)x^2 ) ⇒ W_n =[x (((−1)/(2(n+1))))e^(−(n+1)x^2 ) ]_0 ^∞ −∫_0 ^(+∞) ((−1)/(2(n+1))) e^(−(n+1)x^2 ) dx = (1/(2(n+1)))∫_0 ^∞ e^(−(n+1)x^2 ) dx =_((√(n+1))x =t) (1/(2(n+1))) ∫_0 ^∞ e^(−t^2 ) (dt/( (√(n+1)))) =(1/(2(n+1)(√(n+1)))) ((√π)/2) =((√π)/(4(n+1)^(3/2) )) ⇒ I =Σ_(n=0) ^∞ ((√π)/(4(n+1)^(3/2) )) =((√π)/4) Σ_(n=1) ^∞ (1/n^(3/2) ) I=((√π)/4)ξ((3/2)) rest to calculate ξ((3/2))....be continued...](https://www.tinkutara.com/question/Q61832.png)
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}} }{{e}^{{x}^{\mathrm{2}} } −\mathrm{1}}\:{dx}\:\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } }{\mathrm{1}−{e}^{−{x}^{\mathrm{2}} } }\:{dx}\:=\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{nx}^{\mathrm{2}} } {dx}\right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{x}^{\mathrm{2}} \:{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } {dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{W}_{{n}} \:\:\:{with}\:{W}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{x}^{\mathrm{2}} \:{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \:\:=\int_{\mathrm{0}} ^{\infty} \:{x}\:\left({xe}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \right){dx} \\ $$$${by}\:{parts}\:\:{u}\:={x}\:\:{and}\:{v}^{'} \:={x}\:{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \:\:\:\Rightarrow \\ $$$${W}_{{n}} =\left[{x}\:\left(\frac{−\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\right){e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{+\infty} \:\:\frac{−\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\:{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \:{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } {dx}\:\:=_{\sqrt{{n}+\mathrm{1}}{x}\:={t}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}^{\mathrm{2}} } \frac{{dt}}{\:\sqrt{{n}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)\sqrt{{n}+\mathrm{1}}}\:\frac{\sqrt{\pi}}{\mathrm{2}}\:=\frac{\sqrt{\pi}}{\mathrm{4}\left({n}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\Rightarrow\:{I}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\sqrt{\pi}}{\mathrm{4}\left({n}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\frac{\sqrt{\pi}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${I}=\frac{\sqrt{\pi}}{\mathrm{4}}\xi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:\:\:{rest}\:{to}\:{calculate}\:\xi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)….{be}\:{continued}… \\ $$$$ \\ $$
Commented by Smail last updated on 09/Jun/19
![(1/(e^x^2 −1))=(e^(−x^2 ) /(1−e^(−x^2 ) ))=e^(−x^2 ) Σ_(n=0) ^∞ (e^(−x^2 ) )^n =Σ_(n=0) ^∞ e^(−(n+1)x^2 ) ∣(e^(−(n+2)x^2 ) /e^(−(n+1)x^2 ) )∣=e^(−x^2 ) <1 −x^2 <0⇔x^2 >0 So Σ_(n=0) ^∞ e^(−(n+1)x^2 ) converges at IR/{0} ∫_0 ^∞ (x^2 /(e^x^2 −1))dx=Σ_(n=0) ^∞ ∫_0 ^∞ x^2 e^(−(n+1)x^2 ) dx By parts u=x⇒u′=1 v′=xe^(−(n+1)x^2 ) ⇒v=(1/(−2(n+1)))e^(−(n+1)x^2 ) ∫_0 ^∞ (x^2 /(e^x^2 −1))dx=Σ_(n=0) ^∞ ([((−1)/(2(n+1)))xe^(−(n+1)x^2 ) ]_0 ^∞ +(1/(2(n+1)))∫_0 ^∞ e^(−(n+1)x^2 ) dx) =Σ_(n=0) ^∞ (1/(2(n+1)))∫_0 ^∞ e^(−(n+1)x^2 ) dx Let t=(√(n+1))x⇒dx=(dt/( (√(n+1)))) ∫_0 ^∞ (x^2 /(e^x^2 −1))dx=(1/2)Σ_(n=0) ^∞ (1/((n+1)(√(n+1))))∫_0 ^∞ e^(−t^2 ) dt =((√π)/4)Σ_(n=0) ^∞ (1/((n+1)^(3/2) ))=((√π)/4)Σ_(n=1) ^∞ (1/n^(3/2) ) =((√π)/4)ζ((3/2))](https://www.tinkutara.com/question/Q61833.png)
$$\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{2}} } −\mathrm{1}}=\frac{{e}^{−{x}^{\mathrm{2}} } }{\mathrm{1}−{e}^{−{x}^{\mathrm{2}} } }={e}^{−{x}^{\mathrm{2}} } \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({e}^{−{x}^{\mathrm{2}} } \right)^{{n}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \\ $$$$\mid\frac{{e}^{−\left({n}+\mathrm{2}\right){x}^{\mathrm{2}} } }{{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } }\mid={e}^{−{x}^{\mathrm{2}} } <\mathrm{1} \\ $$$$−{x}^{\mathrm{2}} <\mathrm{0}\Leftrightarrow{x}^{\mathrm{2}} >\mathrm{0} \\ $$$${So}\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \:{converges}\:{at}\:{IR}/\left\{\mathrm{0}\right\} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} }{{e}^{{x}^{\mathrm{2}} } −\mathrm{1}}{dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } {dx} \\ $$$${By}\:{parts}\: \\ $$$${u}={x}\Rightarrow{u}'=\mathrm{1} \\ $$$${v}'={xe}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \Rightarrow{v}=\frac{\mathrm{1}}{−\mathrm{2}\left({n}+\mathrm{1}\right)}{e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} }{{e}^{{x}^{\mathrm{2}} } −\mathrm{1}}{dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left[\frac{−\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}{xe}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } {dx}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} } {dx} \\ $$$${Let}\:\:{t}=\sqrt{{n}+\mathrm{1}}{x}\Rightarrow{dx}=\frac{{dt}}{\:\sqrt{{n}+\mathrm{1}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} }{{e}^{{x}^{\mathrm{2}} } −\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\sqrt{{n}+\mathrm{1}}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{4}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }=\frac{\sqrt{\pi}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{4}}\zeta\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by maxmathsup by imad last updated on 10/Jun/19

$${thanks}\:{sir}\:{Smail}\:… \\ $$
