Question Number 148567 by mathmax by abdo last updated on 29/Jul/21
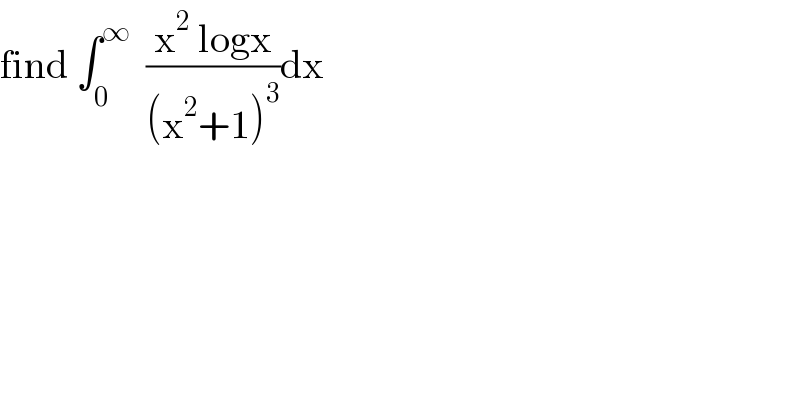
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{logx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$
Answered by Ar Brandon last updated on 29/Jul/21
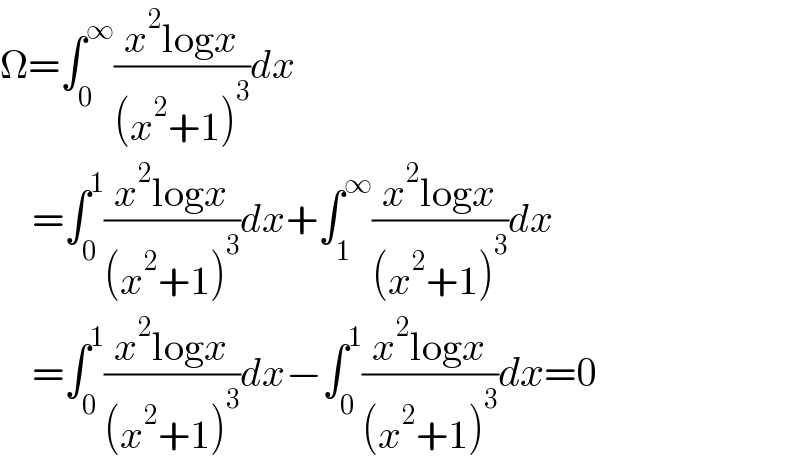
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{log}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \mathrm{log}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx}+\int_{\mathrm{1}} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{log}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \mathrm{log}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \mathrm{log}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx}=\mathrm{0} \\ $$
