Question Number 124061 by Bird last updated on 30/Nov/20
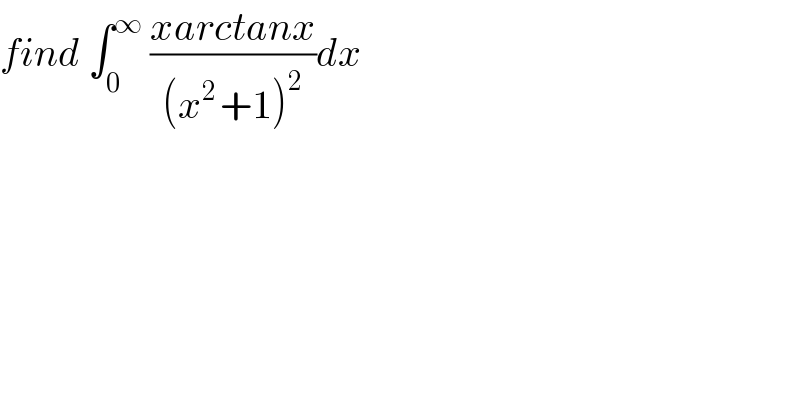
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{xarctanx}}{\left({x}^{\mathrm{2}\:} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by mnjuly1970 last updated on 30/Nov/20
![Ω=[((−1)/(2(x^2 +1)))tan^(−1) (x)]_0 ^∞ +(1/2)∫_0 ^( ∞) (1/((x^2 +1)^2 ))dx =^((x^2 =ξ)) (1/4)∫_0 ^( ∞) (ξ^((−1)/2) /((1+ξ)^2 ))dξ=(1/4)β((1/2),(3/2)) =(1/4) ((Γ((1/2))(1/2)Γ((1/2)))/(Γ(2)))=(π/8) ✓](https://www.tinkutara.com/question/Q124067.png)
$$\Omega=\left[\frac{−\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{tan}^{−\mathrm{1}} \left({x}\right)\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\:\:\overset{\left({x}^{\mathrm{2}} =\xi\right)} {=}\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\infty} \frac{\xi^{\frac{−\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+\xi\right)^{\mathrm{2}} }{d}\xi=\frac{\mathrm{1}}{\mathrm{4}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)}=\frac{\pi}{\mathrm{8}}\:\:\checkmark \\ $$
Answered by Dwaipayan Shikari last updated on 30/Nov/20
![∫_0 ^∞ ((xtan^(−1) x)/((x^2 +1)^2 ))dx tan^(−1) x=θ⇒(1/(1+x^2 ))=(dθ/dx) =∫_0 ^(π/2) ((θtanθ)/(sec^2 θ))dθ =−(θ/4)[cos(2θ)]_0 ^(π/2) +(1/8)[sin2θ]_0 ^(π/2) =(π/8)](https://www.tinkutara.com/question/Q124068.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{{xtan}^{−\mathrm{1}} {x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\:\:\:\:\:\:\:\:\:{tan}^{−\mathrm{1}} {x}=\theta\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{{d}\theta}{{dx}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\theta{tan}\theta}{{sec}^{\mathrm{2}} \theta}{d}\theta \\ $$$$=−\frac{\theta}{\mathrm{4}}\left[{cos}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{8}}\left[{sin}\mathrm{2}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{8}} \\ $$
