Question Number 122157 by mathmax by abdo last updated on 14/Nov/20
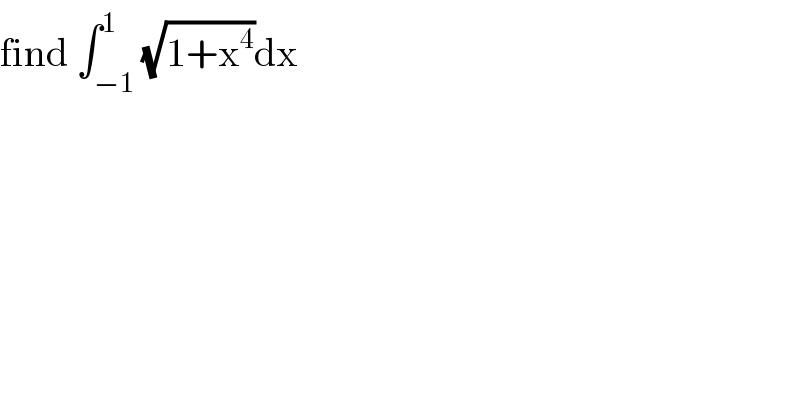
$$\mathrm{find}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$
Commented by peter frank last updated on 14/Nov/20

$$\mathrm{Qn}\:\mathrm{121384} \\ $$
Answered by mindispower last updated on 15/Nov/20

$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$$${x}^{\mathrm{4}} ={u}\Rightarrow{dx}={u}^{−\frac{\mathrm{3}}{\mathrm{4}}} \frac{{du}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{u}}.{u}^{−\frac{\mathrm{3}}{\mathrm{4}}} {du}={I} \\ $$$$\beta\left({b},{c}−{b}\right)_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b},{c};{z}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{b}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{c}−{b}−\mathrm{1}} \left(\mathrm{1}−{zx}\right)^{−{a}} {dx} \\ $$$$\beta\:{betta}\:{function},_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b},{c};{z}\right)\:{Hypergeometric} \\ $$$${function} \\ $$$${I}\Leftrightarrow\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {u}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−{u}\right)^{\mathrm{0}} {du} \\ $$$$\Rightarrow{b}−\mathrm{1}=−\frac{\mathrm{3}}{\mathrm{4}},{c}−{b}−\mathrm{1}=\mathrm{0},−{a}=\frac{\mathrm{1}}{\mathrm{2}},−{z}=\mathrm{1} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{4}},{c}=\frac{\mathrm{5}}{\mathrm{4}},{a}=−\frac{\mathrm{1}}{\mathrm{2}},{z}=−\mathrm{1} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{1}}{\mathrm{4}},\mathrm{1}\right)\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{5}}{\mathrm{4}};−\mathrm{1}\right) \\ $$$$\frac{\beta\left(\frac{\mathrm{1}}{\mathrm{4}},\mathrm{1}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)}\:=\mathrm{2} \\ $$$${we}\:{get}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }{dx}=\mathrm{2}._{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{5}}{\mathrm{4}};−\mathrm{1}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 15/Nov/20
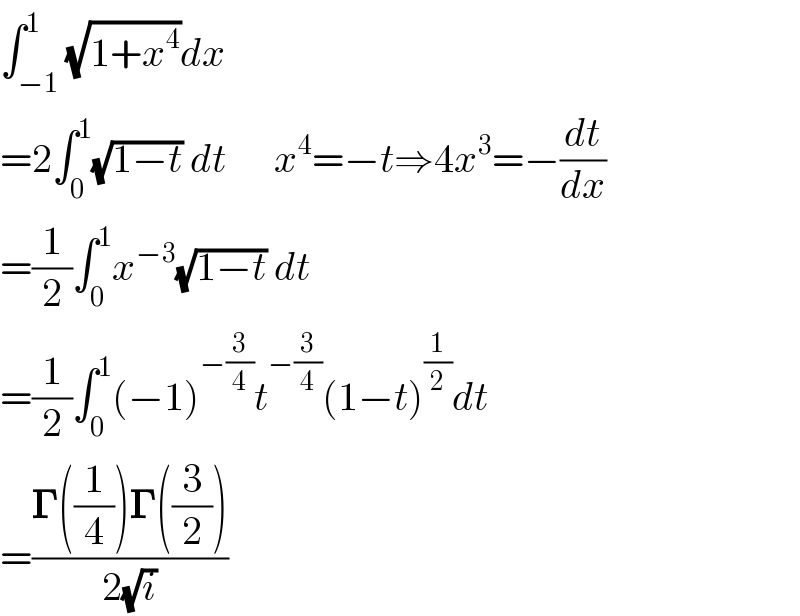
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{t}}\:{dt}\:\:\:\:\:\:{x}^{\mathrm{4}} =−{t}\Rightarrow\mathrm{4}{x}^{\mathrm{3}} =−\frac{{dt}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\mathrm{3}} \sqrt{\mathrm{1}−{t}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} {t}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$=\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}\sqrt{{i}}} \\ $$
