Menu Close

find-1-1-t-2-arctan-t-1-t-dt-

Tinku Tara 0 Comments
Pin




Question Number 42488 by maxmathsup by imad last updated on 26/Aug/18
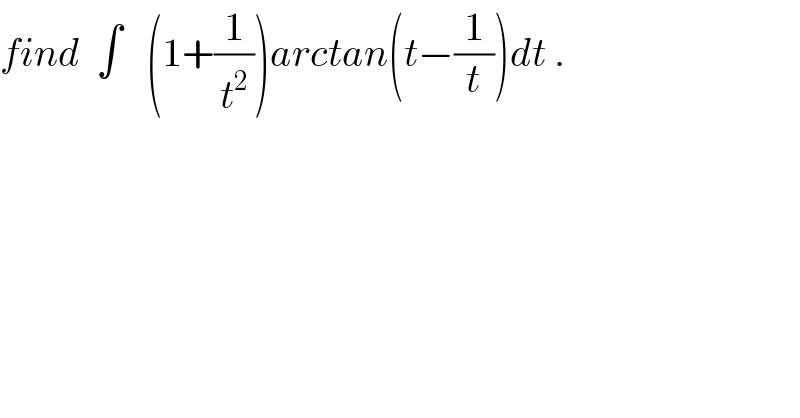
find ∫ (1+(1/t^2 ))arctan(t−(1/t))dt .
$${find}\:\:\int\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){arctan}\left({t}−\frac{\mathrm{1}}{{t}}\right){dt}\:. \\ $$
Commented by maxmathsup by imad last updated on 27/Aug/18
by parts u^′ =1+(1/t^2 ) and v =arctan(t−(1/t)) ⇒ I =(t−(1/t))arctan(t−(1/t)) −∫ (t−(1/t))((1+(1/t^2 ))/(1+(t−(1/t))^2 ))dt =(t−(1/t))arctan(t−(1/t)) −∫ (((t−1)(t^2 +1))/(t^3 ( 1+t^2 −2 +(1/t^2 ))))dt =(t−(1/t))arctan(t−(1/t)) −∫ (((t−1)(t^2 +1))/(t(t^2 +t^4 −2t^2 +1)))dt but ∫ (((t−1)(t^2 +1))/(t(t^2 +t^4 −2t^2 +1)))dt = ∫ ((t^3 +t−t^2 −1)/(t^3 +t^5 −2t^3 +1))dt =∫ ((t^3 −t^2 +t−1)/(t^5 −t^3 +1))dt let decompose F(t) = ((t^3 −t^2 +t−1)/(t^5 −t^3 +1)) the roots of t^5 −t^3 +1 are t_1 ∼0,959+0,4284i (complex) t_2 ∼0,959−0,4284i (complex) t_3 ∼ −1,2365 (reel) t_4 ∼−0,3408 +0,7854 i(complex) t_5 ∼ −0,3408 −0,7854 i (comlex) ⇒ F(t) ∼((t^3 −t^2 +t−1)/((t−t_1 )(t −t_1 ^− )(t−t_3 )(t−t_4 )(t−t_4 ^− ))) ∼((t^3 −t^2 +t−1)/((t−t_3 )(t^2 −2Re(t_1 )t +1)(t^2 −2 Re(t_4 )t +1))) ∼(a/(t−t_3 )) + ((bt +c)/(t^2 −2Re(t_1 )t +1)) + ((dt +e)/(t^2 −2Re(t_4 )t +1)) ⇒ ∫ F(t)dt ∼ ∫ ((adt)/(t−t_3 )) + ∫ ((bt +c)/(t^2 −2Re(t_1 )t +1)) + ∫ ((dt +e)/(t^2 −2Re(t_4 )t +1)) +c... ...be continued...
$${by}\:{parts}\:{u}^{'} \:=\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:{and}\:{v}\:={arctan}\left({t}−\frac{\mathrm{1}}{{t}}\right)\:\Rightarrow \\ $$$${I}\:\:=\left({t}−\frac{\mathrm{1}}{{t}}\right){arctan}\left({t}−\frac{\mathrm{1}}{{t}}\right)\:−\int\:\:\:\left({t}−\frac{\mathrm{1}}{{t}}\right)\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\mathrm{1}+\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} }{dt} \\ $$$$=\left({t}−\frac{\mathrm{1}}{{t}}\right){arctan}\left({t}−\frac{\mathrm{1}}{{t}}\right)\:−\int\:\:\frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{{t}^{\mathrm{3}} \left(\:\:\:\:\mathrm{1}+{t}^{\mathrm{2}} \:−\mathrm{2}\:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)}{dt} \\ $$$$=\left({t}−\frac{\mathrm{1}}{{t}}\right){arctan}\left({t}−\frac{\mathrm{1}}{{t}}\right)\:−\int\:\:\:\:\:\:\frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{{t}\left({t}^{\mathrm{2}} \:+{t}^{\mathrm{4}} \:−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt}\:{but} \\ $$$$\int\:\:\:\frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{{t}\left({t}^{\mathrm{2}} \:+{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt}\:=\:\int\:\:\:\frac{{t}^{\mathrm{3}} \:+{t}−{t}^{\mathrm{2}} \:−\mathrm{1}}{{t}^{\mathrm{3}} \:+{t}^{\mathrm{5}} \:−\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{1}}{dt} \\ $$$$=\int\:\:\:\:\frac{{t}^{\mathrm{3}} \:−{t}^{\mathrm{2}} \:+{t}−\mathrm{1}}{{t}^{\mathrm{5}} \:−{t}^{\mathrm{3}} \:+\mathrm{1}}{dt}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\:\frac{{t}^{\mathrm{3}} −{t}^{\mathrm{2}} \:+{t}−\mathrm{1}}{{t}^{\mathrm{5}} −{t}^{\mathrm{3}} \:+\mathrm{1}} \\ $$$${the}\:{roots}\:{of}\:{t}^{\mathrm{5}} −{t}^{\mathrm{3}} \:+\mathrm{1}\:\:{are} \\ $$$${t}_{\mathrm{1}} \sim\mathrm{0},\mathrm{959}+\mathrm{0},\mathrm{4284}{i}\:\left({complex}\right) \\ $$$${t}_{\mathrm{2}} \:\sim\mathrm{0},\mathrm{959}−\mathrm{0},\mathrm{4284}{i}\:\left({complex}\right) \\ $$$${t}_{\mathrm{3}} \:\sim\:−\mathrm{1},\mathrm{2365}\:\:\:\:\left({reel}\right) \\ $$$${t}_{\mathrm{4}} \:\:\sim−\mathrm{0},\mathrm{3408}\:+\mathrm{0},\mathrm{7854}\:{i}\left({complex}\right) \\ $$$${t}_{\mathrm{5}} \:\sim\:−\mathrm{0},\mathrm{3408}\:−\mathrm{0},\mathrm{7854}\:{i}\:\:\left({comlex}\right)\:\Rightarrow \\ $$$${F}\left({t}\right)\:\:\sim\frac{{t}^{\mathrm{3}} \:−{t}^{\mathrm{2}} \:+{t}−\mathrm{1}}{\left({t}−{t}_{\mathrm{1}} \right)\left({t}\:−\overset{−} {{t}}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{3}} \right)\left({t}−{t}_{\mathrm{4}} \right)\left({t}−\overset{−} {{t}}_{\mathrm{4}} \right)} \\ $$$$\sim\frac{{t}^{\mathrm{3}} \:−{t}^{\mathrm{2}} \:+{t}−\mathrm{1}}{\left({t}−{t}_{\mathrm{3}} \right)\left({t}^{\mathrm{2}} \:−\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:−\mathrm{2}\:{Re}\left({t}_{\mathrm{4}} \right){t}\:+\mathrm{1}\right)} \\ $$$$\sim\frac{{a}}{{t}−{t}_{\mathrm{3}} }\:+\:\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:−\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:+\mathrm{1}}\:+\:\frac{{dt}\:+{e}}{{t}^{\mathrm{2}} \:−\mathrm{2}{Re}\left({t}_{\mathrm{4}} \right){t}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:\:\sim\:\:\int\:\:\:\frac{{adt}}{{t}−{t}_{\mathrm{3}} }\:+\:\int\:\:\:\:\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:−\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:+\mathrm{1}}\:+\:\int\:\:\:\frac{{dt}\:+{e}}{{t}^{\mathrm{2}} \:−\mathrm{2}{Re}\left({t}_{\mathrm{4}} \right){t}\:+\mathrm{1}}\:+{c}… \\ $$$$…{be}\:{continued}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18
y=t−(1/t) dy=1+(1/t^2 )dt ∫tan^(−1) ydy ytan^(−1) y−(1/2)∫((2y)/(1+y^2 ))dy ytan^(−1) y−(1/2)ln(1+y^2 )+c (t−(1/t))tan^(−1) (t−(1/t))−(1/2)ln(1+t^2 −2+(1/t^2 ))+c (t−(1/t))tan^(−1) (t−(1/t))−(1/2)ln(t^2 −1+(1/t^2 ))+c
$${y}={t}−\frac{\mathrm{1}}{{t}}\:\:\:{dy}=\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int{tan}^{−\mathrm{1}} {ydy} \\ $$$${ytan}^{−\mathrm{1}} {y}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{y}}{\mathrm{1}+{y}^{\mathrm{2}} }{dy} \\ $$$${ytan}^{−\mathrm{1}} {y}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)+{c} \\ $$$$\left({t}−\frac{\mathrm{1}}{{t}}\right){tan}^{−\mathrm{1}} \left({t}−\frac{\mathrm{1}}{{t}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)+{c} \\ $$$$\left({t}−\frac{\mathrm{1}}{{t}}\right){tan}^{−\mathrm{1}} \left({t}−\frac{\mathrm{1}}{{t}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *