Menu Close

find-1-1-x-2-ln-1-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 42088 by maxmathsup by imad last updated on 17/Aug/18
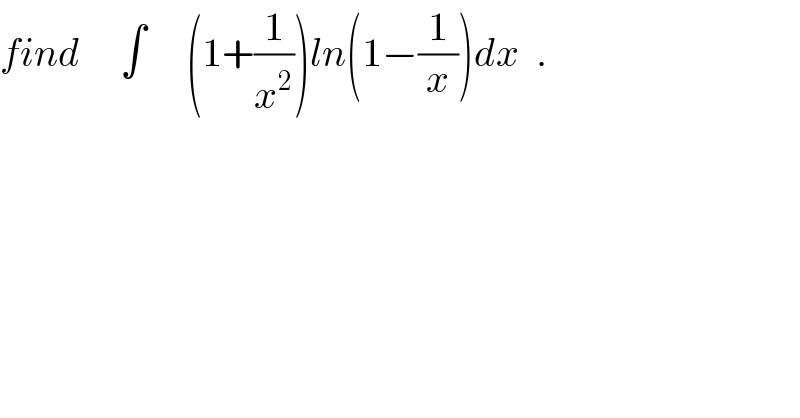
find ∫ (1+(1/x^2 ))ln(1−(1/x))dx .
$${find}\:\:\:\:\:\int\:\:\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx}\:\:. \\ $$
Commented by maxmathsup by imad last updated on 17/Aug/18
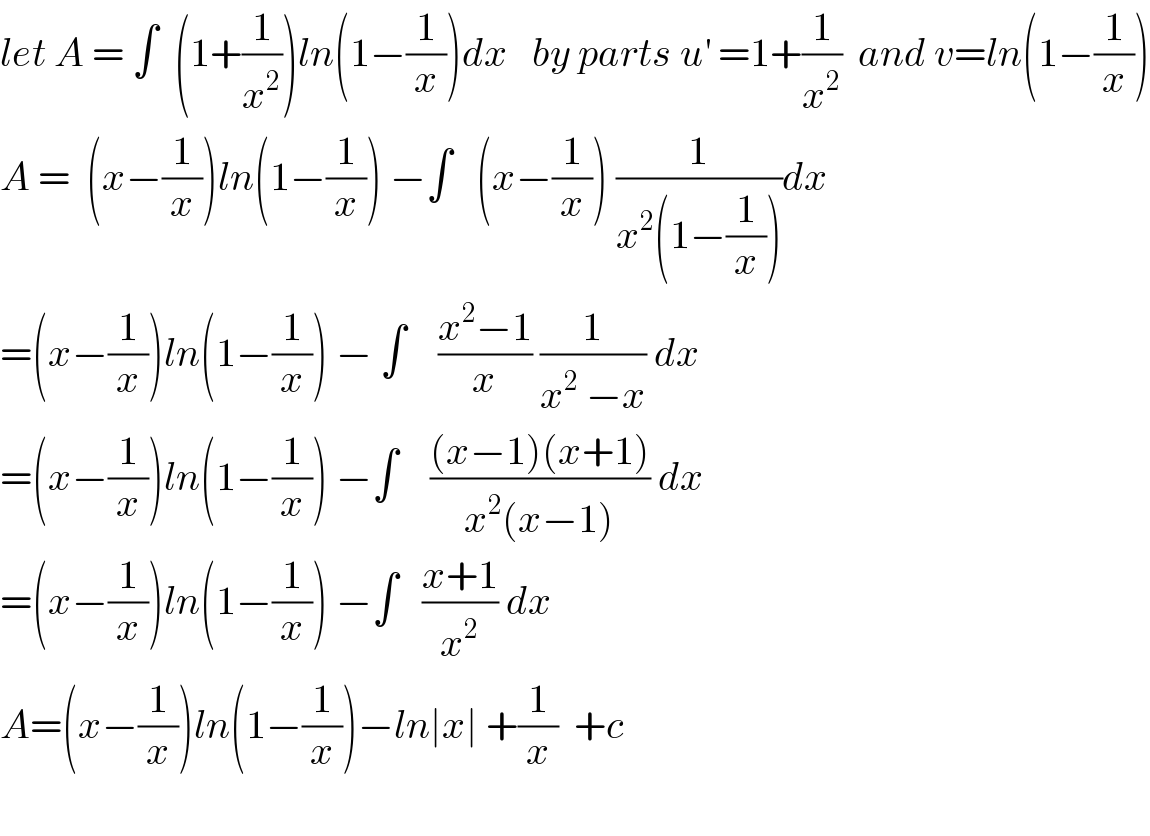
let A = ∫ (1+(1/x^2 ))ln(1−(1/x))dx by parts u^′ =1+(1/x^2 ) and v=ln(1−(1/x)) A = (x−(1/x))ln(1−(1/x)) −∫ (x−(1/x)) (1/(x^2 (1−(1/x))))dx =(x−(1/x))ln(1−(1/x)) − ∫ ((x^2 −1)/x) (1/(x^2 −x)) dx =(x−(1/x))ln(1−(1/x)) −∫ (((x−1)(x+1))/(x^2 (x−1))) dx =(x−(1/x))ln(1−(1/x)) −∫ ((x+1)/x^2 ) dx A=(x−(1/x))ln(1−(1/x))−ln∣x∣ +(1/x) +c
$${let}\:{A}\:=\:\int\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx}\:\:\:{by}\:{parts}\:{u}^{'} \:=\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\:{and}\:{v}={ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${A}\:=\:\:\left({x}−\frac{\mathrm{1}}{{x}}\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\:−\int\:\:\:\left({x}−\frac{\mathrm{1}}{{x}}\right)\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)}{dx} \\ $$$$=\left({x}−\frac{\mathrm{1}}{{x}}\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\:−\:\int\:\:\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:−{x}}\:{dx} \\ $$$$=\left({x}−\frac{\mathrm{1}}{{x}}\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\:−\int\:\:\:\:\frac{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)}\:{dx} \\ $$$$=\left({x}−\frac{\mathrm{1}}{{x}}\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\:−\int\:\:\:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$${A}=\left({x}−\frac{\mathrm{1}}{{x}}\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−{ln}\mid{x}\mid\:+\frac{\mathrm{1}}{{x}}\:\:+{c}\: \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Aug/18
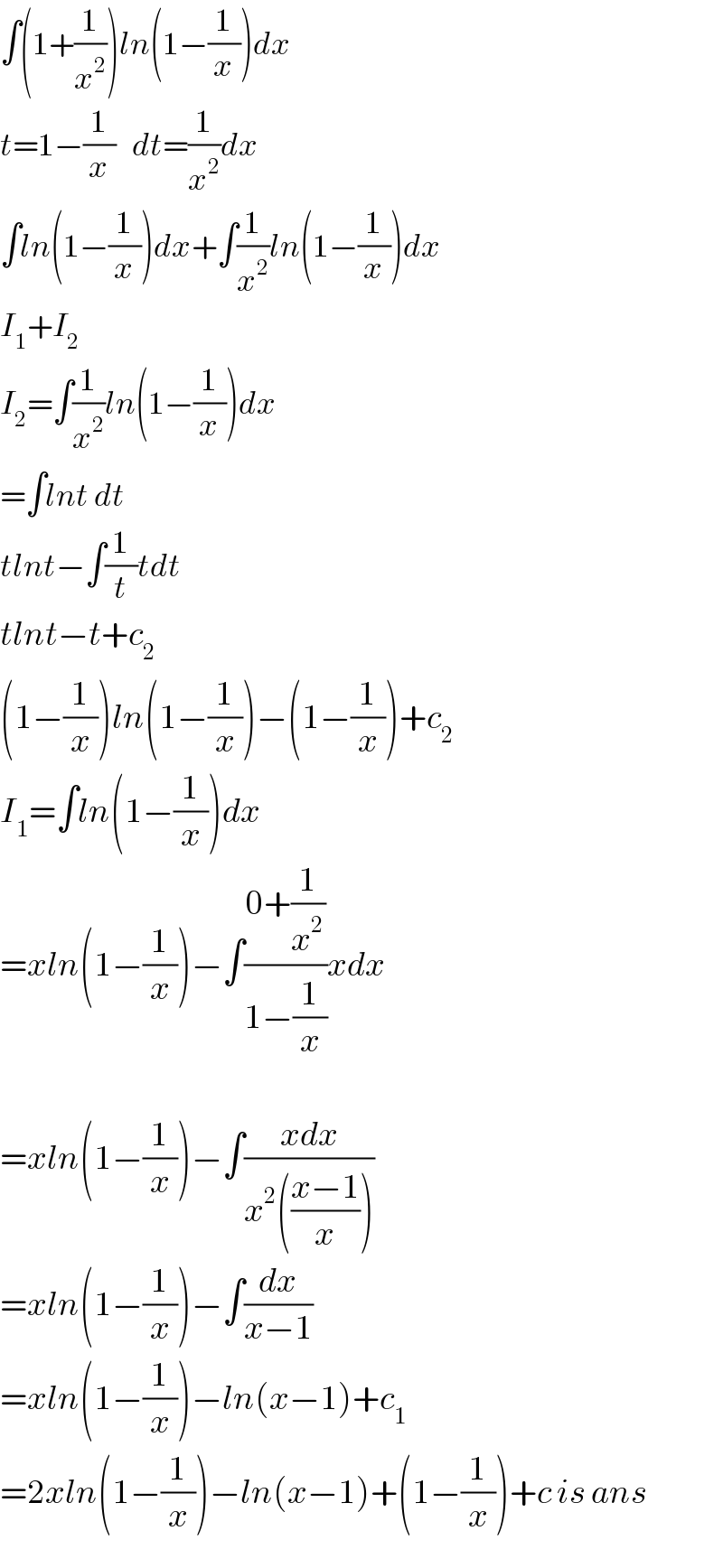
∫(1+(1/x^2 ))ln(1−(1/x))dx t=1−(1/x) dt=(1/x^2 )dx ∫ln(1−(1/x))dx+∫(1/x^2 )ln(1−(1/x))dx I_1 +I_2 I_2 =∫(1/x^2 )ln(1−(1/x))dx =∫lnt dt tlnt−∫(1/t)tdt tlnt−t+c_2 (1−(1/x))ln(1−(1/x))−(1−(1/x))+c_2 I_1 =∫ln(1−(1/x))dx =xln(1−(1/x))−∫((0+(1/x^2 ))/(1−(1/x)))xdx =xln(1−(1/x))−∫((xdx)/(x^2 (((x−1)/x)))) =xln(1−(1/x))−∫(dx/(x−1)) =xln(1−(1/x))−ln(x−1)+c_1 =2xln(1−(1/x))−ln(x−1)+(1−(1/x))+c is ans
$$\int\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$${t}=\mathrm{1}−\frac{\mathrm{1}}{{x}}\:\:\:{dt}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$\int{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx}+\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$$=\int{lnt}\:{dt} \\ $$$${tlnt}−\int\frac{\mathrm{1}}{{t}}{tdt} \\ $$$${tlnt}−{t}+{c}_{\mathrm{2}} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)+{c}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\int{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$$={xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−\int\frac{\mathrm{0}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{1}}{{x}}}{xdx} \\ $$$$ \\ $$$$={xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−\int\frac{{xdx}}{{x}^{\mathrm{2}} \left(\frac{{x}−\mathrm{1}}{{x}}\right)} \\ $$$$={xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−\int\frac{{dx}}{{x}−\mathrm{1}} \\ $$$$={xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−{ln}\left({x}−\mathrm{1}\right)+{c}_{\mathrm{1}} \\ $$$$=\mathrm{2}{xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−{ln}\left({x}−\mathrm{1}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)+{c}\:{is}\:{ans} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *