Menu Close

find-1-dx-x-2-1-x-x-2-

Tinku Tara 0 Comments
Pin




Question Number 64866 by mathmax by abdo last updated on 22/Jul/19
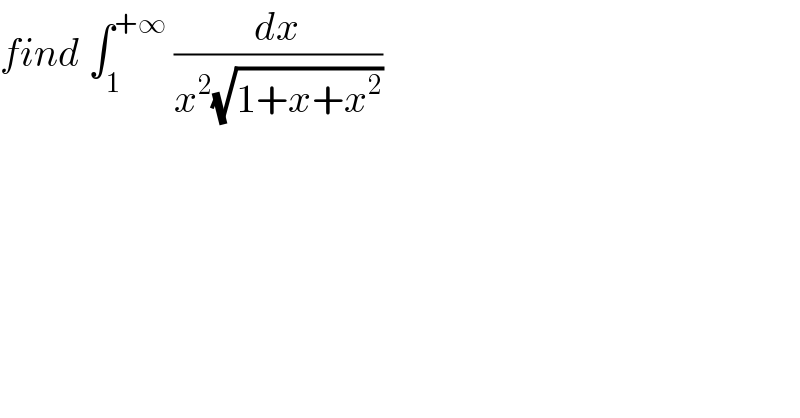
find ∫_1 ^(+∞) (dx/(x^2 (√(1+x+x^2 ))))
$${find}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }} \\ $$
Commented by mathmax by abdo last updated on 23/Jul/19
let A =∫_1 ^(+∞) (dx/(x^2 (√(x^2 +x+1)))) we have x^2 +x+1 =(x+(1/2))^2 +(3/4) changement x+(1/2)=((√3)/2) sh(t) give sh(t)=((2x+1)/( (√3))) A = ∫_(argsh((√3))) ^(+∞) (1/((((√3)/2)sht−(1/2))^2 ((√3)/2)ch(t))) ((√3)/2) ch(t)dt = 4∫_(ln((√3)+(√4))) ^(+∞) (dt/(((√3)sh(t)−1)^2 )) =4 ∫_(ln(2+(√3))) ^(+∞) (dt/(3sh^2 t −2(√3)sht +1)) =4 ∫_(ln(2+(√3))) ^(+∞) (dt/(3((ch(2t)−1)/2)−2(√3)sh(t) +1)) =8∫_(ln(2+(√3))) ^(+∞) (dt/(3ch(2t)−3 −4(√3)sh(t) +2)) =8 ∫_(ln(2+(√3))) ^(+∞) (dt/(3ch(2t)−4(√3)sh(t)−1)) =8 ∫_(ln(2+(√3))) ^(+∞) (dt/(3((e^(2t) +e^(−2t) )/2)−4(√3)((e^t −e^(−t) )/(2 ))−1)) =16 ∫_(ln(2+(√3))) ^(+∞) (dt/(3 e^(2t) +3e^(−2t) −4(√3)e^t +4(√3)e^(−t) −2)) =_(e^t =u) 16 ∫_(2+(√3)) ^(+∞) (du/(u( 3 u^2 +3u^(−2) −4(√3)u +4(√3)u^(−1) −2))) =16 ∫_(2+(√3)) ^(+∞) (du/(3u^3 +3u^(−1) −4(√3)u^2 +4(√3)−2u)) =16 ∫_(2+(√3)) ^(+∞) ((udu)/(3u^4 +3 −4(√3)u^3 +4(√3)u−2u^2 )) let decompose F(u) =(u/(3u^4 −4(√3)u^3 −2u^2 +4(√3)u +3)) ....be continued....
$${let}\:{A}\:=\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\:\:\:{we}\:{have}\:{x}^{\mathrm{2}} \:+{x}+\mathrm{1}\:=\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${changement}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{sh}\left({t}\right)\:{give}\:{sh}\left({t}\right)=\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${A}\:=\:\int_{{argsh}\left(\sqrt{\mathrm{3}}\right)} ^{+\infty} \:\:\:\:\frac{\mathrm{1}}{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sht}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{ch}\left({t}\right){dt} \\ $$$$=\:\mathrm{4}\int_{{ln}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{4}}\right)} ^{+\infty} \:\:\:\:\frac{{dt}}{\left(\sqrt{\mathrm{3}}{sh}\left({t}\right)−\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{4}\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} ^{+\infty} \:\:\frac{{dt}}{\mathrm{3}{sh}^{\mathrm{2}} {t}\:−\mathrm{2}\sqrt{\mathrm{3}}{sht}\:+\mathrm{1}} \\ $$$$=\mathrm{4}\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} ^{+\infty} \:\frac{{dt}}{\mathrm{3}\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)\:+\mathrm{1}} \\ $$$$=\mathrm{8}\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} ^{+\infty} \:\:\:\:\:\frac{{dt}}{\mathrm{3}{ch}\left(\mathrm{2}{t}\right)−\mathrm{3}\:−\mathrm{4}\sqrt{\mathrm{3}}{sh}\left({t}\right)\:+\mathrm{2}} \\ $$$$=\mathrm{8}\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} ^{+\infty} \:\:\frac{{dt}}{\mathrm{3}{ch}\left(\mathrm{2}{t}\right)−\mathrm{4}\sqrt{\mathrm{3}}{sh}\left({t}\right)−\mathrm{1}} \\ $$$$=\mathrm{8}\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} ^{+\infty} \:\:\:\:\:\frac{{dt}}{\mathrm{3}\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}−\mathrm{4}\sqrt{\mathrm{3}}\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}\:}−\mathrm{1}} \\ $$$$=\mathrm{16}\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} ^{+\infty} \:\:\:\:\frac{{dt}}{\mathrm{3}\:{e}^{\mathrm{2}{t}} \:+\mathrm{3}{e}^{−\mathrm{2}{t}} \:−\mathrm{4}\sqrt{\mathrm{3}}{e}^{{t}} \:+\mathrm{4}\sqrt{\mathrm{3}}{e}^{−{t}} \:−\mathrm{2}} \\ $$$$=_{{e}^{{t}} \:={u}} \:\:\:\:\mathrm{16}\:\int_{\mathrm{2}+\sqrt{\mathrm{3}}} ^{+\infty} \:\:\:\:\:\:\:\:\frac{{du}}{{u}\left(\:\mathrm{3}\:{u}^{\mathrm{2}} \:+\mathrm{3}{u}^{−\mathrm{2}} \:−\mathrm{4}\sqrt{\mathrm{3}}{u}\:+\mathrm{4}\sqrt{\mathrm{3}}{u}^{−\mathrm{1}} −\mathrm{2}\right)} \\ $$$$=\mathrm{16}\:\int_{\mathrm{2}+\sqrt{\mathrm{3}}} ^{+\infty} \:\:\:\:\:\:\frac{{du}}{\mathrm{3}{u}^{\mathrm{3}} \:+\mathrm{3}{u}^{−\mathrm{1}} −\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2}{u}} \\ $$$$=\mathrm{16}\:\int_{\mathrm{2}+\sqrt{\mathrm{3}}} ^{+\infty} \:\:\:\frac{{udu}}{\mathrm{3}{u}^{\mathrm{4}} \:+\mathrm{3}\:−\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{3}} \:+\mathrm{4}\sqrt{\mathrm{3}}{u}−\mathrm{2}{u}^{\mathrm{2}} }\:\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\frac{{u}}{\mathrm{3}{u}^{\mathrm{4}} −\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{3}} \:−\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{3}}{u}\:+\mathrm{3}}\:….{be}\:{continued}…. \\ $$$$ \\ $$
Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19
let us change u=(1/x) du=−(dx/x^2 ) then we have I=∫_(0 ) ^1 ((udu)/( (√(1+u+u^2 )))) =(1/2)[∫_0 ^1 ((2u+1)/( (√(1+u+u^2 )))) du −∫_(0 ) ^1 (du/( (√(1+u+u^2 ))))] for the 2^(nd ) integral J we knows that 1+u+u^2 =(3/4)[(((2u+1)/( (√3))))^2 +1] let us change v=arctan(((2u+1)/( (√3)))) dv= (((2/( (√3)))du)/((((2u+1)/( (√3))))^2 +1)) so J=∫_0 ^1 (du/( (√(1+u+u^2 ))))=∫_(π/6) ^(π/3) (√(tan^2 v+1)) dv=∫_(π/6) ^(π/3) (dv/(cosv))=∫_(π/6) ^(π/3) ((cosv dv)/((1−sinv)(1+sinv)))=∫_(π/6) ^(π/3) (1/2).[((cosv)/(1−sinv)) +((cosv)/(1+sinv))]dv =[(1/2)ln∣((1+sinv)/(1−sinv))∣ ]_(π/6) ^(π/3) =ln(((4+2(√3))/3)) Now I=(1/2).( [2(√(1+u+u^2 ))]_0 ^1 − J )=(1/2).[( 2(√(3 )) −2)−ln(((4+2(√3))/3))]
$${let}\:{us}\:{change}\:\:{u}=\frac{\mathrm{1}}{{x}}\:\:\:\:{du}=−\frac{{dx}}{{x}^{\mathrm{2}} }\:\:\:\:\:\: \\ $$$${then}\:\:{we}\:{have}\:{I}=\int_{\mathrm{0}\:\:} ^{\mathrm{1}} \frac{{udu}}{\:\sqrt{\mathrm{1}+{u}+{u}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{1}+{u}+{u}^{\mathrm{2}} }}\:{du}\:−\int_{\mathrm{0}\:} ^{\mathrm{1}} \frac{{du}}{\:\sqrt{\mathrm{1}+{u}+{u}^{\mathrm{2}} }}\right] \\ $$$${for}\:{the}\:\mathrm{2}^{{nd}\:} \:\:{integral}\:{J}\:{we}\:{knows}\:{that}\:\mathrm{1}+{u}+{u}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}}\left[\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}\right] \\ $$$${let}\:{us}\:{change}\:{v}={arctan}\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\:\:\:{dv}=\:\frac{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{du}}{\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${so} \\ $$$${J}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{\:\sqrt{\mathrm{1}+{u}+{u}^{\mathrm{2}} }}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{{tan}^{\mathrm{2}} {v}+\mathrm{1}}\:{dv}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{{dv}}{{cosv}}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{cosv}\:{dv}}{\left(\mathrm{1}−{sinv}\right)\left(\mathrm{1}+{sinv}\right)}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{1}}{\mathrm{2}}.\left[\frac{{cosv}}{\mathrm{1}−{sinv}}\:+\frac{{cosv}}{\mathrm{1}+{sinv}}\right]{dv} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{sinv}}{\mathrm{1}−{sinv}}\mid\:\right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} ={ln}\left(\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right) \\ $$$${Now}\:\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}.\left(\:\left[\mathrm{2}\sqrt{\mathrm{1}+{u}+{u}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:−\:{J}\:\right)=\frac{\mathrm{1}}{\mathrm{2}}.\left[\left(\:\mathrm{2}\sqrt{\mathrm{3}\:}\:−\mathrm{2}\right)−{ln}\left(\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\right] \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 28/Jul/19
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *