Question Number 32305 by abdo imad last updated on 22/Mar/18
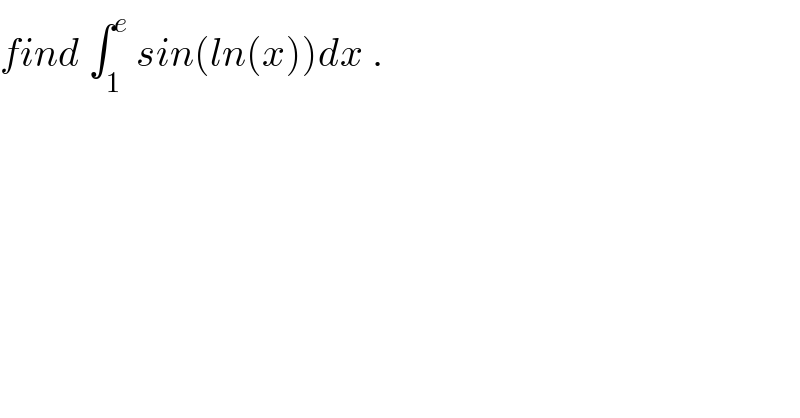
$${find}\:\int_{\mathrm{1}} ^{{e}} \:{sin}\left({ln}\left({x}\right)\right){dx}\:. \\ $$
Commented by abdo imad last updated on 24/Mar/18
![let use the ch.lnx=t ⇒ I = ∫_0 ^1 sint e^t dt and I =Im (∫_0 ^1 e^(it +t) dt) =Im( ∫_0 ^1 e^((1+i)t) dt) but ∫_0 ^1 e^((1+i)t) dt = (1/(1+i))[ e^((1+i)t) ]_0 ^1 = (1/(1+i))( e^(1+i) −1) =((1−i)/2)( e( cos(1) +isin(1) −1) =((e cos(1) +ie sin(1) −1 −ie cos(1) +sin(1) +i)/2) =((e cos(1) +sin(1)−1 +i(e sin(1) −e cos(1) +1))/2) I = (1/2)( e sin(1)−e cos(1) +1) .](https://www.tinkutara.com/question/Q32411.png)
$${let}\:{use}\:{the}\:{ch}.{lnx}={t}\:\Rightarrow\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{sint}\:{e}^{{t}} \:{dt}\:\:{and}\: \\ $$$${I}\:={Im}\:\left(\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{{it}\:+{t}} {dt}\right)\:={Im}\left(\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{\left(\mathrm{1}+{i}\right){t}} {dt}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{\left(\mathrm{1}+{i}\right){t}} {dt}\:=\:\frac{\mathrm{1}}{\mathrm{1}+{i}}\left[\:\:{e}^{\left(\mathrm{1}+{i}\right){t}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{1}+{i}}\left(\:{e}^{\mathrm{1}+{i}} \:−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}−{i}}{\mathrm{2}}\left(\:{e}\left(\:{cos}\left(\mathrm{1}\right)\:+{isin}\left(\mathrm{1}\right)\:−\mathrm{1}\right)\right. \\ $$$$=\frac{{e}\:{cos}\left(\mathrm{1}\right)\:+{ie}\:{sin}\left(\mathrm{1}\right)\:−\mathrm{1}\:−{ie}\:{cos}\left(\mathrm{1}\right)\:+{sin}\left(\mathrm{1}\right)\:+{i}}{\mathrm{2}} \\ $$$$=\frac{{e}\:{cos}\left(\mathrm{1}\right)\:+{sin}\left(\mathrm{1}\right)−\mathrm{1}\:+{i}\left({e}\:{sin}\left(\mathrm{1}\right)\:−{e}\:{cos}\left(\mathrm{1}\right)\:+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\:{e}\:{sin}\left(\mathrm{1}\right)−{e}\:{cos}\left(\mathrm{1}\right)\:+\mathrm{1}\right)\:. \\ $$
Answered by sma3l2996 last updated on 23/Mar/18
![u=sin(lnx)⇒u′=(1/x)cos(lnx) v′=1⇒v=x so ∫_1 ^e sin(lnx)dx=[xsin(lnx)]_1 ^e −∫_1 ^e cos(lnx)dx =esin(1)−∫_1 ^e cos(lnx)dx u=cos(lnx)⇒u′=−(1/x)sin(lnx) v′=1⇒v=x ∫_1 ^e sin(lnx)dx=e.sin(1)−[xcos(lnx)]_1 ^e −∫_1 ^e sin(lnx)dx 2∫_1 ^e sin(lnx)dx=e.sin(1)−e.cos(1)+1 ∫_1 ^e sin(lnx)dx=(e/2)(sin1−cos1)+(1/2)](https://www.tinkutara.com/question/Q32325.png)
$${u}={sin}\left({lnx}\right)\Rightarrow{u}'=\frac{\mathrm{1}}{{x}}{cos}\left({lnx}\right) \\ $$$${v}'=\mathrm{1}\Rightarrow{v}={x} \\ $$$${so}\:\:\int_{\mathrm{1}} ^{{e}} {sin}\left({lnx}\right){dx}=\left[{xsin}\left({lnx}\right)\right]_{\mathrm{1}} ^{{e}} −\int_{\mathrm{1}} ^{{e}} {cos}\left({lnx}\right){dx} \\ $$$$={esin}\left(\mathrm{1}\right)−\int_{\mathrm{1}} ^{{e}} {cos}\left({lnx}\right){dx} \\ $$$${u}={cos}\left({lnx}\right)\Rightarrow{u}'=−\frac{\mathrm{1}}{{x}}{sin}\left({lnx}\right) \\ $$$${v}'=\mathrm{1}\Rightarrow{v}={x} \\ $$$$\int_{\mathrm{1}} ^{{e}} {sin}\left({lnx}\right){dx}={e}.{sin}\left(\mathrm{1}\right)−\left[{xcos}\left({lnx}\right)\right]_{\mathrm{1}} ^{{e}} −\int_{\mathrm{1}} ^{{e}} {sin}\left({lnx}\right){dx} \\ $$$$\mathrm{2}\int_{\mathrm{1}} ^{{e}} {sin}\left({lnx}\right){dx}={e}.{sin}\left(\mathrm{1}\right)−{e}.{cos}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$$\int_{\mathrm{1}} ^{{e}} {sin}\left({lnx}\right){dx}=\frac{{e}}{\mathrm{2}}\left({sin}\mathrm{1}−{cos}\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by abdo imad last updated on 24/Mar/18
$${correct}\:{answer}\:{thanks}… \\ $$
