Menu Close

Find-1-sin-2-6-1-sin-2-42-1-sin-2-66-1-sin-2-78-

Tinku Tara 0 Comments
Pin




Question Number 155724 by mathdanisur last updated on 03/Oct/21
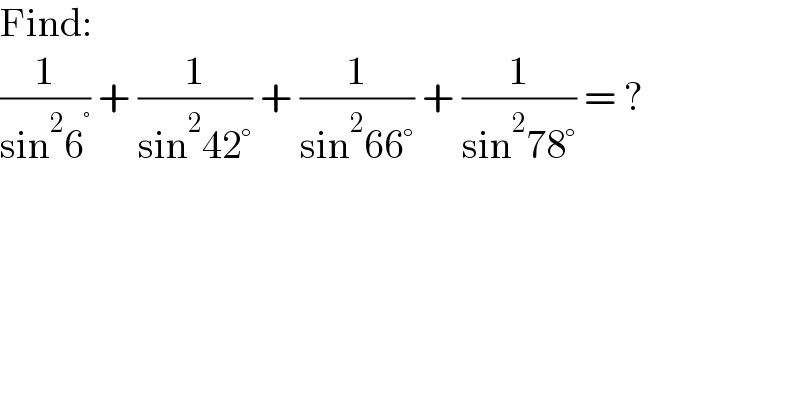
Find: (1/(sin^2 6^° )) + (1/(sin^2 42°)) + (1/(sin^2 66°)) + (1/(sin^2 78°)) = ?
$$\mathrm{Find}: \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{6}^{°} }\:+\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{42}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{66}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{78}°}\:=\:? \\ $$
Answered by som(math1967) last updated on 04/Oct/21
(1/(sin^2 6)) +(1/(sin^2 66)) ((2sin^2 66+2sin^2 6)/(2sin^2 6sin^2 66)) =((1−cos132+1−cos12)/(2sin^2 6sin^2 66)) =((2+cos48−cos12)/(2sin^2 6sin^2 66)) =((2+2sin30sin(−18))/(2sin^2 6sin^2 66)) =((2(1−(((√5)−1)/8)))/(2sin^2 6sin^2 66)) =((9−(√5))/(2(2sin6sin66)^2 )) =((9−(√5))/((cos60−cos72)^2 )) =((9−(√5))/(2((1/2)−(((√5)−1)/4))^2 ))=((8(9−(√5)))/((3−(√5))^2 ))=((8(9−(√5)))/(14−6(√5))) =((4(9−(√5)))/(7−3(√5)))=((4(9−(√5))(7+3(√5)))/(7−3(√5))) again (1/(sin^2 42))+(1/(sin^2 78)) ((1−cos84+1−cos156)/(2sin^2 42sin^2 78)) =((2+cos24−cos84)/(2sin^2 42sin^2 78)) ((2+2sin54sin30)/(2sin^2 42sin^2 78)) =((2(1+(((√5)+1)/8)))/(2sin^2 42sin^2 78)) =((9+(√5))/(2(2sin42sin78)^2 ))=((9+(√5))/(2(cos36−cos120)^2 )) =((9+(√5))/(2((((√5)+1)/4)+(1/2))^2 )) =((8(9+(√5)))/((3+(√5))^2 ))=((8(9+(√5)))/(14+6(√5)))=((4(9+(√5))(7−3(√5)))/((7+3(√5))(7−3(√5)))) ∴(1/(sin^2 6^° )) + (1/(sin^2 42°)) + (1/(sin^2 66°)) + (1/(sin^2 78°)) =(4/4)(63−15+9(√5)+63−15−9(√5)) =126−30=96 ans
$$\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \mathrm{6}}\:+\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \mathrm{66}} \\ $$$$\frac{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{66}+\mathrm{2}{sin}^{\mathrm{2}} \mathrm{6}}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{6}{sin}^{\mathrm{2}} \mathrm{66}} \\ $$$$=\frac{\mathrm{1}−{cos}\mathrm{132}+\mathrm{1}−{cos}\mathrm{12}}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{6}{sin}^{\mathrm{2}} \mathrm{66}} \\ $$$$=\frac{\mathrm{2}+{cos}\mathrm{48}−{cos}\mathrm{12}}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{6}{sin}^{\mathrm{2}} \mathrm{66}} \\ $$$$=\frac{\mathrm{2}+\mathrm{2}{sin}\mathrm{30}{sin}\left(−\mathrm{18}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{6}{sin}^{\mathrm{2}} \mathrm{66}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{8}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{6}{sin}^{\mathrm{2}} \mathrm{66}} \\ $$$$=\frac{\mathrm{9}−\sqrt{\mathrm{5}}}{\mathrm{2}\left(\mathrm{2}{sin}\mathrm{6}{sin}\mathrm{66}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{9}−\sqrt{\mathrm{5}}}{\left({cos}\mathrm{60}−{cos}\mathrm{72}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{9}−\sqrt{\mathrm{5}}}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }=\frac{\mathrm{8}\left(\mathrm{9}−\sqrt{\mathrm{5}}\right)}{\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }=\frac{\mathrm{8}\left(\mathrm{9}−\sqrt{\mathrm{5}}\right)}{\mathrm{14}−\mathrm{6}\sqrt{\mathrm{5}}}\: \\ $$$$=\frac{\mathrm{4}\left(\mathrm{9}−\sqrt{\mathrm{5}}\right)}{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}}=\frac{\mathrm{4}\left(\mathrm{9}−\sqrt{\mathrm{5}}\right)\left(\mathrm{7}+\mathrm{3}\sqrt{\mathrm{5}}\right)}{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}} \\ $$$${again} \\ $$$$\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \mathrm{42}}+\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \mathrm{78}} \\ $$$$\frac{\mathrm{1}−{cos}\mathrm{84}+\mathrm{1}−{cos}\mathrm{156}}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{42}{sin}^{\mathrm{2}} \mathrm{78}} \\ $$$$=\frac{\mathrm{2}+{cos}\mathrm{24}−{cos}\mathrm{84}}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{42}{sin}^{\mathrm{2}} \mathrm{78}} \\ $$$$\frac{\mathrm{2}+\mathrm{2}{sin}\mathrm{54}{sin}\mathrm{30}}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{42}{sin}^{\mathrm{2}} \mathrm{78}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}+\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{8}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \mathrm{42}{sin}^{\mathrm{2}} \mathrm{78}} \\ $$$$=\frac{\mathrm{9}+\sqrt{\mathrm{5}}}{\mathrm{2}\left(\mathrm{2}{sin}\mathrm{42}{sin}\mathrm{78}\right)^{\mathrm{2}} }=\frac{\mathrm{9}+\sqrt{\mathrm{5}}}{\mathrm{2}\left({cos}\mathrm{36}−{cos}\mathrm{120}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{9}+\sqrt{\mathrm{5}}}{\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{8}\left(\mathrm{9}+\sqrt{\mathrm{5}}\right)}{\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }=\frac{\mathrm{8}\left(\mathrm{9}+\sqrt{\mathrm{5}}\right)}{\mathrm{14}+\mathrm{6}\sqrt{\mathrm{5}}}=\frac{\mathrm{4}\left(\mathrm{9}+\sqrt{\mathrm{5}}\right)\left(\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}\right)}{\left(\mathrm{7}+\mathrm{3}\sqrt{\mathrm{5}}\right)\left(\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}\right)} \\ $$$$\therefore\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{6}^{°} }\:+\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{42}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{66}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{78}°}\: \\ $$$$=\frac{\mathrm{4}}{\mathrm{4}}\left(\mathrm{63}−\mathrm{15}+\mathrm{9}\sqrt{\mathrm{5}}+\mathrm{63}−\mathrm{15}−\mathrm{9}\sqrt{\mathrm{5}}\right) \\ $$$$=\mathrm{126}−\mathrm{30}=\mathrm{96}\:{ans} \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 04/Oct/21
thanks
$$\mathrm{thanks} \\ $$
Commented by Tawa11 last updated on 04/Oct/21
Weldone sir.
$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *