Question Number 94114 by naka3546 last updated on 16/May/20
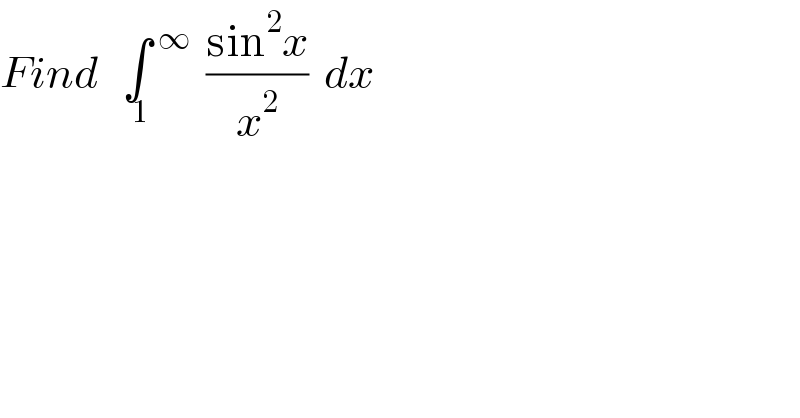
$${Find}\:\:\:\underset{\:\mathrm{1}} {\int}\overset{\:\infty} {\:}\:\:\frac{\mathrm{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }\:\:{dx}\:\: \\ $$
Commented by mathmax by abdo last updated on 17/May/20
![I =∫_1 ^∞ ((sin^2 x)/x^2 )dx we have ∫_0 ^∞ ((sin^2 x)/x^2 )dx =∫_0 ^1 ((sin^2 x)/x^2 )dx +∫_1 ^∞ ((sin^2 x)/x^2 )dx ⇒I =∫_0 ^∞ ((sin^2 x)/x^2 )dx −∫_0 ^1 ((sin^2 x)/x^2 )dx but ∫_0 ^∞ ((sin^2 x)/x^2 )dx =_(by parts) [−(1/x)sin^2 x]_0 ^∞ +∫_0 ^∞ (1/x)(2sinx cosx)dx =∫_0 ^∞ (1/x)sin(2x)dx =_(2x =t) ∫_0 ^∞ ((sint)/(t/2))×(dt/2) =∫_0 ^∞ ((sint)/t)dt =(π/2) ⇒ I =(π/2) −∫_0 ^1 ((1−cos(2x))/x^2 )dx we have cos(2x) =Σ_(n=0) ^∞ (((−1)^n )/((2n)!))(2x)^(2n) =Σ_(n=0) ^∞ ((2^(2n) (−1)^n )/((2n)!)) x^(2n) =1+Σ_(n=1) ^∞ (((−1)^n 4^n )/((2n)!)) x^(2n) ⇒1−cosx =−Σ_(n=1) ^∞ (((−1)^n 4^n )/((2n)!)) x^(2n) ⇒ ((1−cosx)/x^2 ) =Σ_(n=1) ^∞ (((−1)^(n−1) 4^n )/((2n)!)) x^(2n−2) ⇒ ∫_0 ^1 ((1−cosx)/x^2 )dx =Σ_(n=1) ^∞ (((−1)^(n−1) 4^n )/((2n)!))[(1/(2n−1))x^(2n−1) ]_0 ^1 =Σ_(n=1) ^∞ (((−1)^(n−1) 4^n )/((2n−1)(2n)!)) ⇒ I =(π/2) +Σ_(n=1) ^∞ (((−1)^n 4^n )/((2n−1)(2n)!)) I =(π/2)−(4/(2!)) +(4^2 /(3(4)!))−(4^3 /(5(6)!)) +.... we can take n=4 or 5 for approximate value .](https://www.tinkutara.com/question/Q94128.png)
$${I}\:=\int_{\mathrm{1}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}\:\:\:{we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}\:=_{{by}\:{parts}} \:\:\left[−\frac{\mathrm{1}}{{x}}{sin}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\infty} \:+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{x}}\left(\mathrm{2}{sinx}\:{cosx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{x}}{sin}\left(\mathrm{2}{x}\right){dx}\:=_{\mathrm{2}{x}\:={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{sint}}{\frac{{t}}{\mathrm{2}}}×\frac{{dt}}{\mathrm{2}}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{sint}}{{t}}{dt}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\frac{\pi}{\mathrm{2}}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} }{dx}\:\:{we}\:{have} \\ $$$${cos}\left(\mathrm{2}{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!}\left(\mathrm{2}{x}\right)^{\mathrm{2}{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{2}{n}} \left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!}\:{x}^{\mathrm{2}{n}} \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}\right)!}\:{x}^{\mathrm{2}{n}} \:\Rightarrow\mathrm{1}−{cosx}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}\right)!}\:{x}^{\mathrm{2}{n}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}−{cosx}}{{x}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \mathrm{4}^{{n}} }{\left(\mathrm{2}{n}\right)!}\:{x}^{\mathrm{2}{n}−\mathrm{2}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{cosx}}{{x}^{\mathrm{2}} }{dx}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}\right)!}\left[\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}{x}^{\mathrm{2}{n}−\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}\right)!}\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}\right)!} \\ $$$${I}\:=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{2}!}\:+\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{4}\right)!}−\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{5}\left(\mathrm{6}\right)!}\:+…. \\ $$$${we}\:{can}\:{take}\:{n}=\mathrm{4}\:{or}\:\mathrm{5}\:{for}\:{approximate}\:{value}\:. \\ $$
