Question Number 90752 by abdomathmax last updated on 25/Apr/20
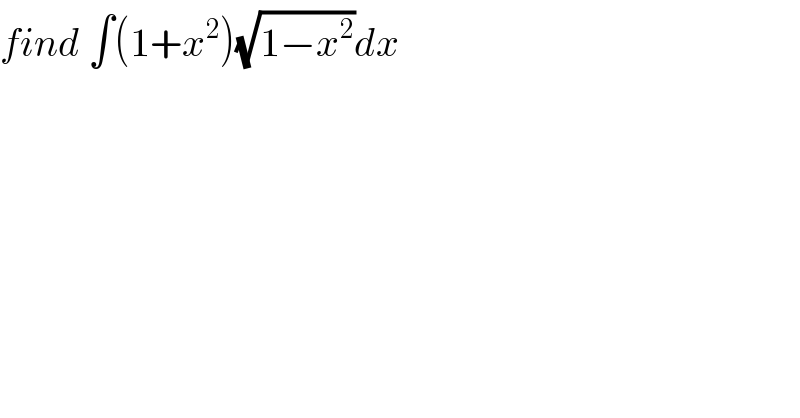
$${find}\:\int\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$
Answered by MJS last updated on 25/Apr/20
![∫(1+x^2 )(√(1−x^2 ))dx= [t=arcsin x → dx=(√(1−x^2 ))dt] =∫(1−sin^4 t)dt=∫((5/8)+(1/2)cos 2t −(1/8)cos 4t)dt= =(5/8)t+(1/4)sin 2t −(1/(32))sin 4t = =(5/8)t+(1/8)(sin t (3+2sin^2 t)cos t)= =(5/8)arcsin x +(1/8)x(2x^2 +3)(√(1−x^2 )) +C](https://www.tinkutara.com/question/Q90756.png)
$$\int\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:{x}\:\rightarrow\:{dx}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dt}\right] \\ $$$$=\int\left(\mathrm{1}−\mathrm{sin}^{\mathrm{4}} \:{t}\right){dt}=\int\left(\frac{\mathrm{5}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{t}\:−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\:\mathrm{4}{t}\right){dt}= \\ $$$$=\frac{\mathrm{5}}{\mathrm{8}}{t}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{t}\:−\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin}\:\mathrm{4}{t}\:= \\ $$$$=\frac{\mathrm{5}}{\mathrm{8}}{t}+\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{sin}\:{t}\:\left(\mathrm{3}+\mathrm{2sin}^{\mathrm{2}} \:{t}\right)\mathrm{cos}\:{t}\right)= \\ $$$$=\frac{\mathrm{5}}{\mathrm{8}}\mathrm{arcsin}\:{x}\:+\frac{\mathrm{1}}{\mathrm{8}}{x}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+{C} \\ $$
Commented by mathmax by abdo last updated on 25/Apr/20
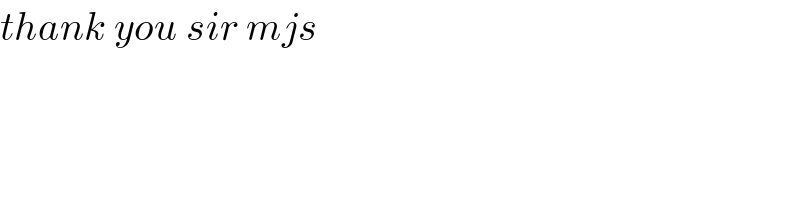
$${thank}\:{you}\:{sir}\:{mjs} \\ $$
Commented by peter frank last updated on 26/Apr/20

$${thanks} \\ $$
Commented by peter frank last updated on 26/Apr/20

$${help}\:\mathrm{90240} \\ $$
