Question Number 31090 by abdo imad last updated on 02/Mar/18
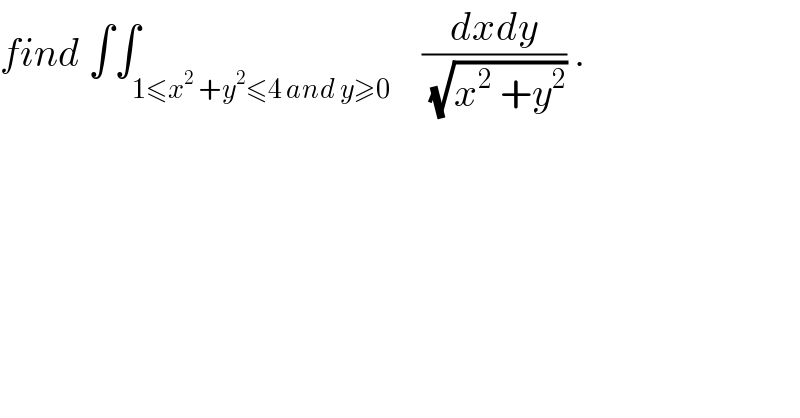
$${find}\:\int\int_{\mathrm{1}\leqslant{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \leqslant\mathrm{4}\:{and}\:{y}\geqslant\mathrm{0}} \:\:\:\frac{{dxdy}}{\:\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}\:. \\ $$
Commented by abdo imad last updated on 06/Mar/18
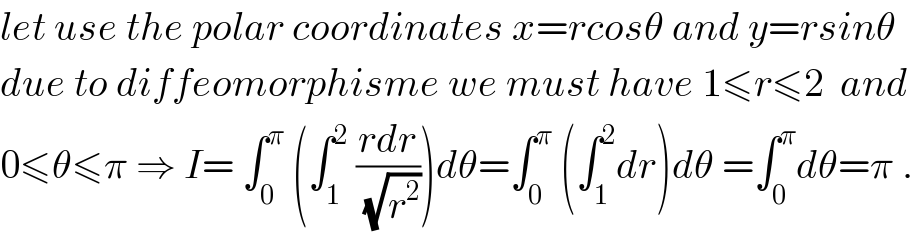
$${let}\:{use}\:{the}\:{polar}\:{coordinates}\:{x}={rcos}\theta\:{and}\:{y}={rsin}\theta \\ $$$${due}\:{to}\:{diffeomorphisme}\:{we}\:{must}\:{have}\:\mathrm{1}\leqslant{r}\leqslant\mathrm{2}\:\:{and} \\ $$$$\mathrm{0}\leqslant\theta\leqslant\pi\:\Rightarrow\:{I}=\:\int_{\mathrm{0}} ^{\pi} \:\left(\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{rdr}}{\:\sqrt{{r}^{\mathrm{2}} }}\right){d}\theta=\int_{\mathrm{0}} ^{\pi} \:\left(\int_{\mathrm{1}} ^{\mathrm{2}} {dr}\right){d}\theta\:=\int_{\mathrm{0}} ^{\pi} {d}\theta=\pi\:. \\ $$
