Question Number 146361 by gsk2684 last updated on 13/Jul/21
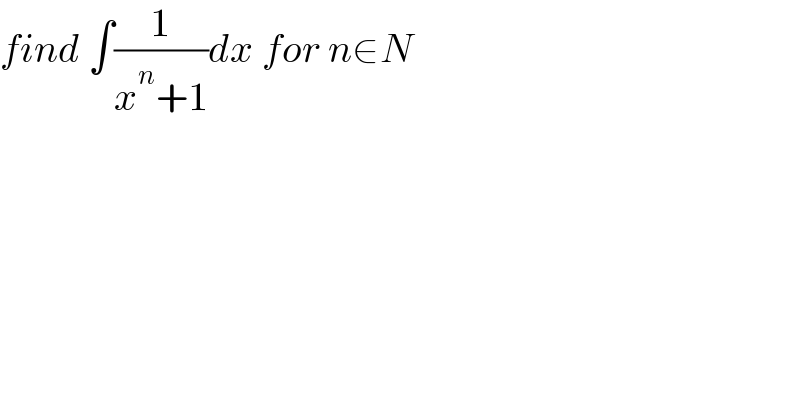
$${find}\:\int\frac{\mathrm{1}}{{x}^{{n}} +\mathrm{1}}{dx}\:{for}\:{n}\in{N} \\ $$
Answered by mathmax by abdo last updated on 13/Jul/21

$$\mathrm{z}^{\mathrm{n}} \:+\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{z}^{\mathrm{n}} \:=\mathrm{e}^{\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{i}\pi} \:\Rightarrow\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\frac{\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{i}\pi}{\mathrm{n}}} \:\mathrm{and}\:\mathrm{o}\leqslant\mathrm{k}\leqslant\mathrm{n}−\mathrm{1}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} \:+\mathrm{1}}=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{nz}_{\mathrm{k}} ^{\mathrm{n}−\mathrm{1}} }=−\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} +\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\:\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\Rightarrow\int\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{n}} \:+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \mathrm{z}_{\mathrm{k}} \mathrm{log}\left(\mathrm{z}−\mathrm{z}_{\mathrm{k}} \right)+\mathrm{K} \\ $$
Commented by gsk2684 last updated on 13/Jul/21

$${kindly}\:{explain}\:{second}\:{step}\: \\ $$$${how}\:{could}\:{you}\:{make}\:{decomposition} \\ $$
Commented by mathmax by abdo last updated on 13/Jul/21

$$\mathrm{if}\:\frac{\mathrm{p}\left(\mathrm{x}\right)}{\mathrm{q}\left(\mathrm{x}\right)}=\Sigma\:\frac{\mathrm{a}_{\mathrm{i}} }{\mathrm{x}−\mathrm{x}_{\mathrm{i}} }\:\:\mathrm{with}\:\mathrm{degp}<\mathrm{degq}\:\:\:\mathrm{and}\:\mathrm{x}_{\mathrm{i}} \mathrm{simples}\:\mathrm{roots} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{i}} =\frac{\mathrm{p}\left(\mathrm{x}_{\mathrm{i}} \right)}{\mathrm{q}^{'} \left(\mathrm{x}_{\mathrm{i}} \right)} \\ $$
Commented by gsk2684 last updated on 14/Jul/21

$${thank}\:{you}\: \\ $$
Answered by Snail last updated on 13/Jul/21
![∫((x^(n−1) dx)/(x^(n−1) (x^n +1))) =(1/n)∫(( dt)/(1+(1/t))) where x^n =t(let) =(1/n)[∫dt−∫(dt/(t+1))] =(1/n)[t−ln(t+1)+C] =(1/n)[x^n −ln(x^n +1)]+C](https://www.tinkutara.com/question/Q146437.png)
$$\int\frac{{x}^{{n}−\mathrm{1}} {dx}}{{x}^{{n}−\mathrm{1}} \left({x}^{{n}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{{n}}\int\frac{\:{dt}}{\mathrm{1}+\frac{\mathrm{1}}{{t}}}\:\:\:\:\:{where}\:\:{x}^{{n}} ={t}\left({let}\right) \\ $$$$=\frac{\mathrm{1}}{{n}}\left[\int{dt}−\int\frac{{dt}}{{t}+\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{1}}{{n}}\left[{t}−{ln}\left({t}+\mathrm{1}\right)+{C}\right] \\ $$$$=\frac{\mathrm{1}}{{n}}\left[{x}^{{n}} −{ln}\left({x}^{{n}} +\mathrm{1}\right)\right]+{C} \\ $$
Commented by gsk2684 last updated on 14/Jul/21

$${how}\:{could}\:{you}\:{write}\:{second}\:{step}?\:{please} \\ $$
