Question Number 30182 by abdo imad last updated on 17/Feb/18
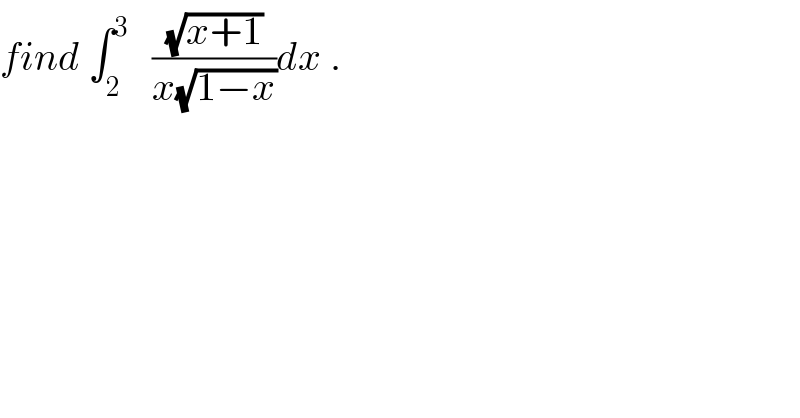
$${find}\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\frac{\sqrt{{x}+\mathrm{1}}}{{x}\sqrt{\mathrm{1}−{x}}}{dx}\:. \\ $$
Commented by abdo imad last updated on 21/Feb/18
![let put (√((x+1)/(x−1))) =t ⇔((x+1)/(x−1)) =t^2 ⇔x+1=−t^2 +t^2 x⇔ (1−t^2 )x=−t^2 −1 ⇔x= ((−t^2 −1)/(−t^2 +1))=((t^2 +1)/(t^2 −1))=1+(2/(t^2 −1))⇒ (dx/dt) =((−4t)/((t^2 −1)^2 )) ⇒I= ∫_(√3) ^(√2) t ((t^2 −1)/(t^2 +1)) ((−4t)/((t^2 −1)^2 ))dt =4 ∫_(√2) ^(√3) (t^2 /((t^2 +1)(t^2 −1)))dt= 4 ∫_(√2) ^(√3) ((t^2 −1+1)/((t^2 +1)(t^2 −1)))dt =4 ∫_(√2) ^(√3) (dt/(t^2 +1)) +4 ∫_(√2) ^(√3) (dt/((t^2 +1)(t^2 −1))) we have ∫_(√2) ^(√3) (dt/(1+t^2 ))=arctan((√3)) −arctan((√2)) and ∫_(√2) ^(√3) (dt/((t^2 +1)(t^2 −1)))=(1/2)∫_(√2) ^(√3) ( (1/(t^2 −1)) −(1/(t^2 +1)))dt =(1/2) ∫_(√2) ^(√3) (dt/(t^2 −1)) −(1/2) (arctan((√(3))) −arctan(√2))) =(1/2)∫_(√2) ^(√3) ((1/(t−1)) −(1/(t+1)))dt −(1/2)(....) =(1/2)[ln∣((t−1)/(t+1))∣]_(√2) ^(√3) −(1/2)(...) ⇒ I=4(artan((√3))−arctan((√2))) +2 ∫_(√2) ^(√3) (dt/(t^2 −1))dt −2(arctan((√3))−arctan((√2))) =2(arctan((√3))−arctan((√2))) +ln∣(((√3) −1)/( (√3)+1))∣−ln∣(((√2) −1)/( (√2) +1))∣ .](https://www.tinkutara.com/question/Q30345.png)
$${let}\:{put}\:\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\:={t}\:\Leftrightarrow\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\:={t}^{\mathrm{2}} \:\:\Leftrightarrow{x}+\mathrm{1}=−{t}^{\mathrm{2}} \:+{t}^{\mathrm{2}} {x}\Leftrightarrow \\ $$$$\left(\mathrm{1}−{t}^{\mathrm{2}} \right){x}=−{t}^{\mathrm{2}} −\mathrm{1}\:\Leftrightarrow{x}=\:\frac{−{t}^{\mathrm{2}} −\mathrm{1}}{−{t}^{\mathrm{2}} +\mathrm{1}}=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}=\mathrm{1}+\frac{\mathrm{2}}{{t}^{\mathrm{2}} −\mathrm{1}}\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{−\mathrm{4}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{I}=\:\int_{\sqrt{\mathrm{3}}} ^{\sqrt{\mathrm{2}}} \:\:\:{t}\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\frac{−\mathrm{4}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\:\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{dt}=\:\mathrm{4}\:\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{dt} \\ $$$$=\mathrm{4}\:\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\:+\mathrm{4}\:\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)}\:{we}\:{have} \\ $$$$\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }={arctan}\left(\sqrt{\mathrm{3}}\right)\:−{arctan}\left(\sqrt{\mathrm{2}}\right)\:{and} \\ $$$$\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\:\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \left(\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}\:−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\left({arctan}\left(\sqrt{\left.\mathrm{3}\right)}\:−{arctan}\sqrt{\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \left(\frac{\mathrm{1}}{{t}−\mathrm{1}}\:−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(….\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\right]_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:−\frac{\mathrm{1}}{\mathrm{2}}\left(…\right)\:\Rightarrow \\ $$$${I}=\mathrm{4}\left({artan}\left(\sqrt{\mathrm{3}}\right)−{arctan}\left(\sqrt{\mathrm{2}}\right)\right)\:+\mathrm{2}\:\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\: \\ $$$$−\mathrm{2}\left({arctan}\left(\sqrt{\mathrm{3}}\right)−{arctan}\left(\sqrt{\mathrm{2}}\right)\right) \\ $$$$=\mathrm{2}\left({arctan}\left(\sqrt{\mathrm{3}}\right)−{arctan}\left(\sqrt{\mathrm{2}}\right)\right)\:+{ln}\mid\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\mid−{ln}\mid\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\:\sqrt{\mathrm{2}}\:+\mathrm{1}}\mid\:\:. \\ $$$$ \\ $$
Commented by abdo imad last updated on 21/Feb/18
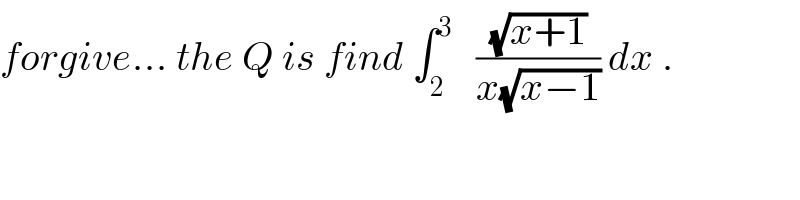
$${forgive}…\:{the}\:{Q}\:{is}\:{find}\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\frac{\sqrt{{x}+\mathrm{1}}}{{x}\sqrt{{x}−\mathrm{1}}}\:{dx}\:. \\ $$
