Menu Close

find-2-tan-2-d-

Tinku Tara 0 Comments
Pin




Question Number 45519 by maxmathsup by imad last updated on 14/Oct/18
find ∫ (√(2+tan^2 θ))dθ
$${find}\:\:\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}{d}\theta \\ $$
Commented by Meritguide1234 last updated on 14/Oct/18
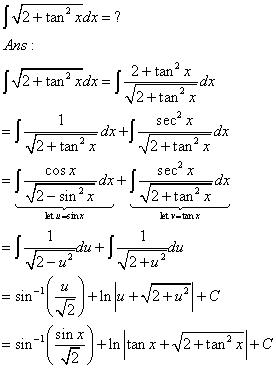
Commented by maxmathsup by imad last updated on 14/Oct/18
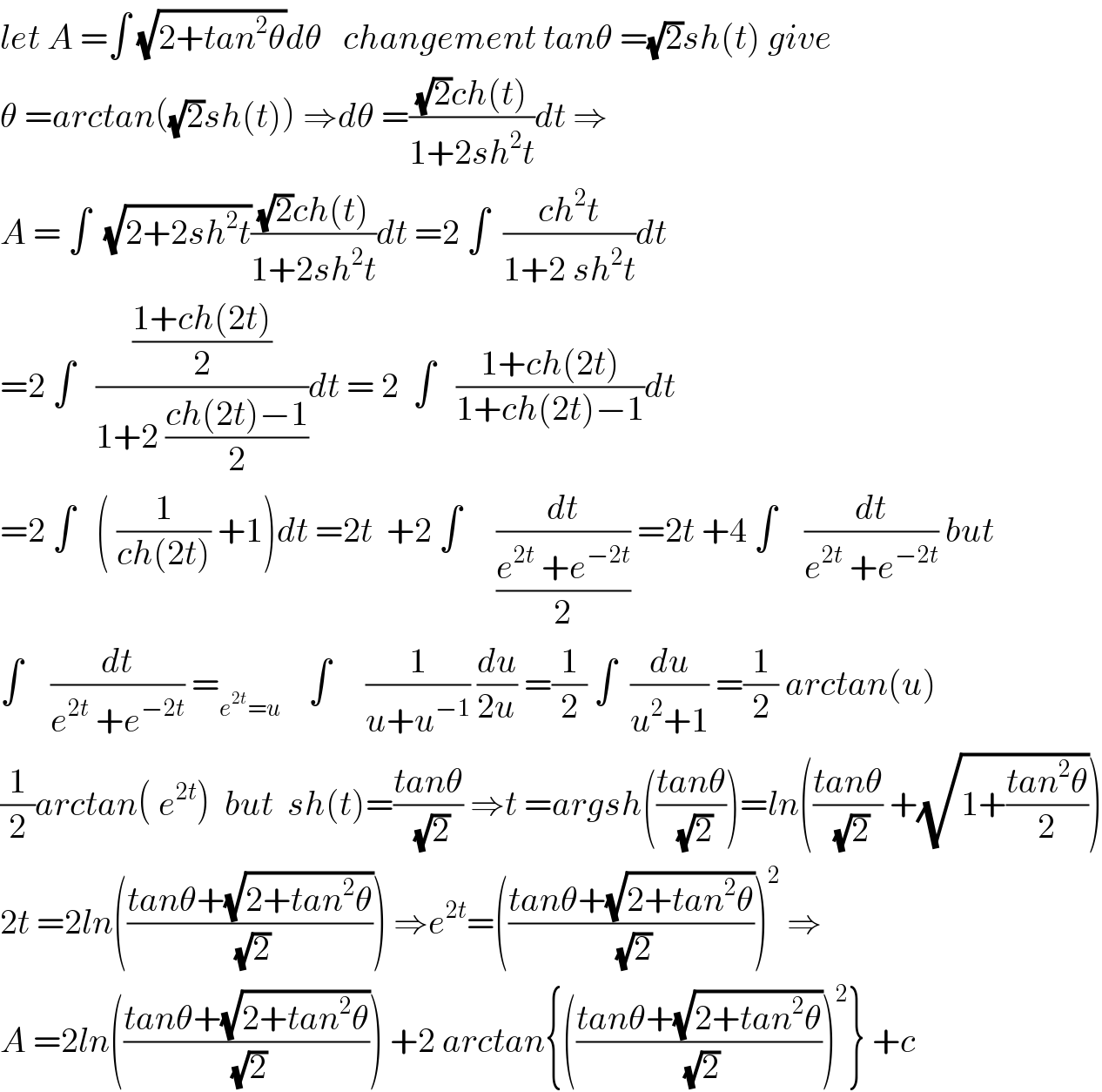
let A =∫ (√(2+tan^2 θ))dθ changement tanθ =(√2)sh(t) give θ =arctan((√2)sh(t)) ⇒dθ =(((√2)ch(t))/(1+2sh^2 t))dt ⇒ A = ∫ (√(2+2sh^2 t))(((√2)ch(t))/(1+2sh^2 t))dt =2 ∫ ((ch^2 t)/(1+2 sh^2 t))dt =2 ∫ (((1+ch(2t))/2)/(1+2 ((ch(2t)−1)/2)))dt = 2 ∫ ((1+ch(2t))/(1+ch(2t)−1))dt =2 ∫ ( (1/(ch(2t))) +1)dt =2t +2 ∫ (dt/((e^(2t) +e^(−2t) )/2)) =2t +4 ∫ (dt/(e^(2t) +e^(−2t) )) but ∫ (dt/(e^(2t) +e^(−2t) )) =_(e^(2t) =u) ∫ (1/(u+u^(−1) )) (du/(2u)) =(1/2) ∫ (du/(u^2 +1)) =(1/2) arctan(u) (1/2)arctan( e^(2t) ) but sh(t)=((tanθ)/( (√2))) ⇒t =argsh(((tanθ)/( (√2))))=ln(((tanθ)/( (√2))) +(√(1+((tan^2 θ)/2)))) 2t =2ln(((tanθ+(√(2+tan^2 θ)))/( (√2)))) ⇒e^(2t) =(((tanθ+(√(2+tan^2 θ)))/( (√2))))^2 ⇒ A =2ln(((tanθ+(√(2+tan^2 θ)))/( (√2)))) +2 arctan{(((tanθ+(√(2+tan^2 θ)))/( (√2))))^2 } +c
$${let}\:{A}\:=\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}{d}\theta\:\:\:{changement}\:{tan}\theta\:=\sqrt{\mathrm{2}}{sh}\left({t}\right)\:{give} \\ $$$$\theta\:={arctan}\left(\sqrt{\mathrm{2}}{sh}\left({t}\right)\right)\:\Rightarrow{d}\theta\:=\frac{\sqrt{\mathrm{2}}{ch}\left({t}\right)}{\mathrm{1}+\mathrm{2}{sh}^{\mathrm{2}} {t}}{dt}\:\Rightarrow \\ $$$${A}\:=\:\int\:\:\sqrt{\mathrm{2}+\mathrm{2}{sh}^{\mathrm{2}} {t}}\frac{\sqrt{\mathrm{2}}{ch}\left({t}\right)}{\mathrm{1}+\mathrm{2}{sh}^{\mathrm{2}} {t}}{dt}\:=\mathrm{2}\:\int\:\:\frac{{ch}^{\mathrm{2}} {t}}{\mathrm{1}+\mathrm{2}\:{sh}^{\mathrm{2}} {t}}{dt} \\ $$$$=\mathrm{2}\:\int\:\:\:\frac{\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}{\mathrm{1}+\mathrm{2}\:\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}}{dt}\:=\:\mathrm{2}\:\:\int\:\:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{dt} \\ $$$$=\mathrm{2}\:\int\:\:\:\left(\:\frac{\mathrm{1}}{{ch}\left(\mathrm{2}{t}\right)}\:+\mathrm{1}\right){dt}\:=\mathrm{2}{t}\:\:+\mathrm{2}\:\int\:\:\:\:\:\frac{{dt}}{\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}\:=\mathrm{2}{t}\:+\mathrm{4}\:\int\:\:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }\:{but} \\ $$$$\int\:\:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }\:=_{{e}^{\mathrm{2}{t}} ={u}} \:\:\:\:\int\:\:\:\:\:\frac{\mathrm{1}}{{u}+{u}^{−\mathrm{1}} }\:\frac{{du}}{\mathrm{2}{u}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left({u}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\:{e}^{\mathrm{2}{t}} \right)\:\:{but}\:\:{sh}\left({t}\right)=\frac{{tan}\theta}{\:\sqrt{\mathrm{2}}}\:\Rightarrow{t}\:={argsh}\left(\frac{{tan}\theta}{\:\sqrt{\mathrm{2}}}\right)={ln}\left(\frac{{tan}\theta}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\mathrm{1}+\frac{{tan}^{\mathrm{2}} \theta}{\mathrm{2}}}\right) \\ $$$$\mathrm{2}{t}\:=\mathrm{2}{ln}\left(\frac{{tan}\theta+\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}}{\:\sqrt{\mathrm{2}}}\right)\:\Rightarrow{e}^{\mathrm{2}{t}} =\left(\frac{{tan}\theta+\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${A}\:=\mathrm{2}{ln}\left(\frac{{tan}\theta+\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}}{\:\sqrt{\mathrm{2}}}\right)\:+\mathrm{2}\:{arctan}\left\{\left(\frac{{tan}\theta+\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} \theta}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \right\}\:+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *