find-2-x-2-x-dx-

Question Number 60494 by Mr X pcx last updated on 21/May/19

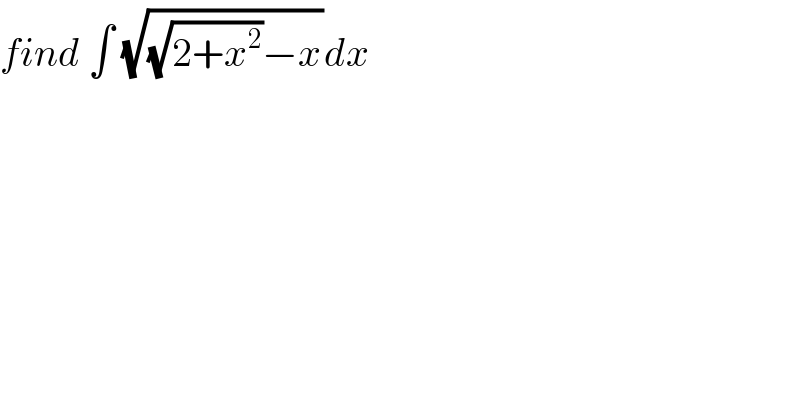
$${find}\:\int\:\sqrt{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }−{x}}{dx} \\ $$

Commented by maxmathsup by imad last updated on 22/May/19

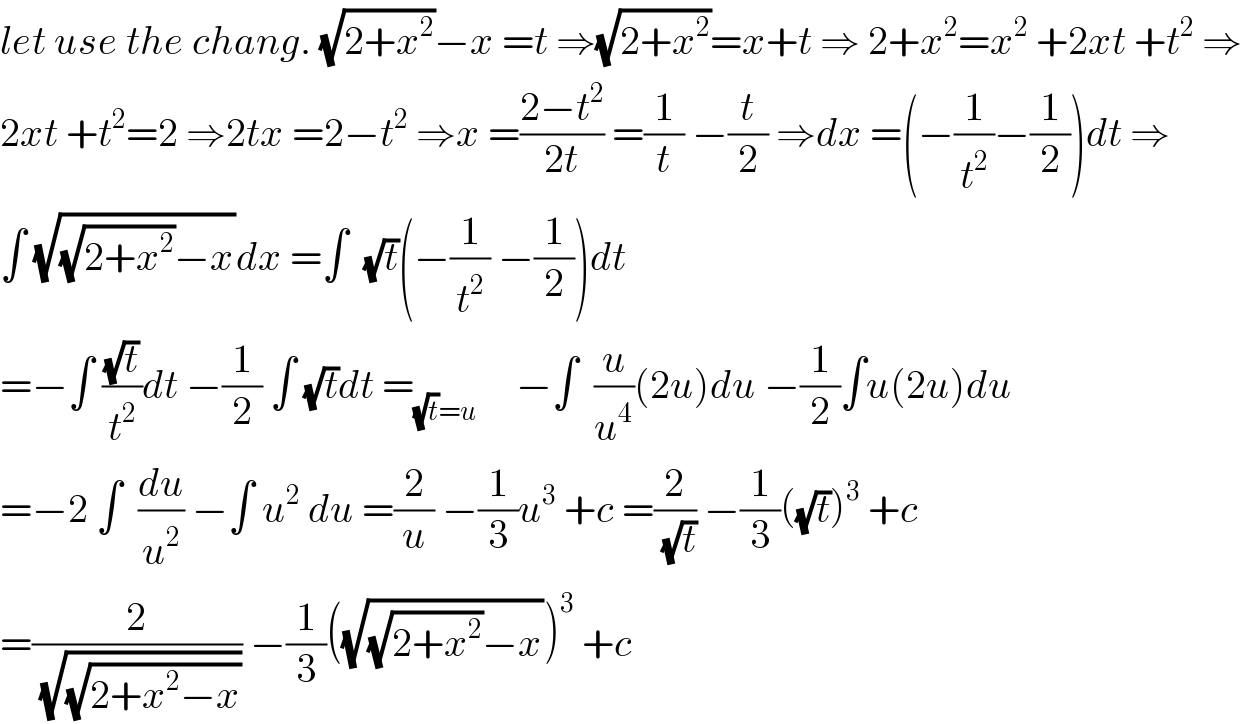
let use the chang. (√(2+x^2 ))−x =t ⇒(√(2+x^2 ))=x+t ⇒ 2+x^2 =x^2 +2xt +t^2 ⇒ 2xt +t^2 =2 ⇒2tx =2−t^2 ⇒x =((2−t^2 )/(2t)) =(1/t) −(t/2) ⇒dx =(−(1/t^2 )−(1/2))dt ⇒ ∫ (√((√(2+x^2 ))−x))dx =∫ (√t)(−(1/t^2 ) −(1/2))dt =−∫ ((√t)/t^2 )dt −(1/2) ∫ (√t)dt =_((√t)=u) −∫ (u/u^4 )(2u)du −(1/2)∫u(2u)du =−2 ∫ (du/u^2 ) −∫ u^2 du =(2/u) −(1/3)u^3 +c =(2/( (√t))) −(1/3)((√t))^3 +c =(2/( (√(√(2+x^2 −x))))) −(1/3)((√((√(2+x^2 ))−x)))^3 +c

$${let}\:{use}\:{the}\:{chang}.\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }−{x}\:={t}\:\Rightarrow\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }={x}+{t}\:\Rightarrow\:\mathrm{2}+{x}^{\mathrm{2}} ={x}^{\mathrm{2}} \:+\mathrm{2}{xt}\:+{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{2}{xt}\:+{t}^{\mathrm{2}} =\mathrm{2}\:\Rightarrow\mathrm{2}{tx}\:=\mathrm{2}−{t}^{\mathrm{2}} \:\Rightarrow{x}\:=\frac{\mathrm{2}−{t}^{\mathrm{2}} }{\mathrm{2}{t}}\:=\frac{\mathrm{1}}{{t}}\:−\frac{{t}}{\mathrm{2}}\:\Rightarrow{dx}\:=\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\right){dt}\:\Rightarrow \\ $$$$\int\:\sqrt{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }−{x}}{dx}\:=\int\:\:\sqrt{{t}}\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\right){dt} \\ $$$$=−\int\:\frac{\sqrt{{t}}}{{t}^{\mathrm{2}} }{dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\sqrt{{t}}{dt}\:=_{\sqrt{{t}}={u}} \:\:\:\:\:−\int\:\:\frac{{u}}{{u}^{\mathrm{4}} }\left(\mathrm{2}{u}\right){du}\:−\frac{\mathrm{1}}{\mathrm{2}}\int{u}\left(\mathrm{2}{u}\right){du} \\ $$$$=−\mathrm{2}\:\int\:\:\frac{{du}}{{u}^{\mathrm{2}} }\:−\int\:{u}^{\mathrm{2}} \:{du}\:=\frac{\mathrm{2}}{{u}}\:−\frac{\mathrm{1}}{\mathrm{3}}{u}^{\mathrm{3}} \:+{c}\:=\frac{\mathrm{2}}{\:\sqrt{{t}}}\:−\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{{t}}\right)^{\mathrm{3}} \:+{c} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} −{x}}}}\:−\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }−{x}}\right)^{\mathrm{3}} \:+{c} \\ $$

Answered by MJS last updated on 21/May/19

∫(√((√(x^2 +2))−x))dx= [t=(√((√(x^2 +2))−x)) → dx=−((2(√(x^2 +2)))/( (√((√(x^2 +2))−x))))dt] [⇒ x=((2−t^4 )/(2t^2 )) ⇒ dx=−((t^4 +2)/t^3 )dt] =−∫((t^4 +2)/t^2 )dt=−∫t^2 dt−2∫(dt/t^2 )=−(t^3 /3)+(2/t)= =((6−t^4 )/(3t))=(2/3)(x(√((√(x^2 +2))−x))+(2/( (√((√(x^2 +2))−x)))))+C

$$\int\sqrt{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}−{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}−{x}}\:\rightarrow\:{dx}=−\frac{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}{\:\sqrt{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}−{x}}}{dt}\right] \\ $$$$\:\:\:\:\:\left[\Rightarrow\:{x}=\frac{\mathrm{2}−{t}^{\mathrm{4}} }{\mathrm{2}{t}^{\mathrm{2}} }\:\Rightarrow\:{dx}=−\frac{{t}^{\mathrm{4}} +\mathrm{2}}{{t}^{\mathrm{3}} }{dt}\right] \\ $$$$=−\int\frac{{t}^{\mathrm{4}} +\mathrm{2}}{{t}^{\mathrm{2}} }{dt}=−\int{t}^{\mathrm{2}} {dt}−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} }=−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}}{{t}}= \\ $$$$=\frac{\mathrm{6}−{t}^{\mathrm{4}} }{\mathrm{3}{t}}=\frac{\mathrm{2}}{\mathrm{3}}\left({x}\sqrt{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}−{x}}+\frac{\mathrm{2}}{\:\sqrt{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}−{x}}}\right)+{C} \\ $$

Commented by maxmathsup by imad last updated on 22/May/19

$${thanks}\:{sir}\:{mjs}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply