Question Number 29444 by prof Abdo imad last updated on 08/Feb/18
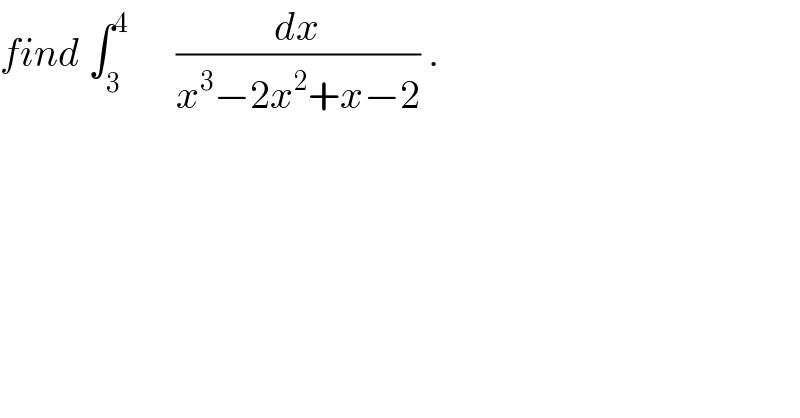
$${find}\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{2}}\:. \\ $$
Commented by prof Abdo imad last updated on 07/Mar/18
![we have x^3 −2x^2 +x−2=x^2 (x−2) +x−2 =(x−2)(x^2 +1)let decompose F(x)= (1/((x−2)(x^2 +1)))=(a/(x−2)) +((bx+c)/(x^2 +1)) a=lim_(x→2) (x−2)F(x)=(1/5) lim_(x→+∞) xF(x)=0=a+b⇒b=−(1/5) so F(x)= (1/(5(x−2))) +((−(1/5)x +c)/(x^2 +1)) F(0)=((−1)/(10)) +c ⇒ F(x)= (1/(5(x−2))) −(1/(10)) ((2x−1)/(x^2 +1)) ∫_3 ^4 F(x)dx= ∫_3 ^4 (dx/(5(x−2))) −(1/(10)) ∫_3 ^4 ((2x)/(x^2 +1)) +(1/(10))∫_3 ^4 (dx/(1+x^2 )) =(1/5)[ln∣x−2∣]_3 ^4 −(1/(10))[ln(x^2 +1)]_3 ^4 +(1/(10)) [arctanx]_3 ^4 =((ln2)/5) −(1/(10))(ln(17)−ln(10))+(1/(10))(arctan4−arctam3).](https://www.tinkutara.com/question/Q31357.png)
$${we}\:{have}\:{x}^{\mathrm{3}} \:−\mathrm{2}{x}^{\mathrm{2}} \:+{x}−\mathrm{2}={x}^{\mathrm{2}} \left({x}−\mathrm{2}\right)\:+{x}−\mathrm{2} \\ $$$$=\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){let}\:{decompose} \\ $$$${F}\left({x}\right)=\:\:\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{a}}{{x}−\mathrm{2}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}={lim}_{{x}\rightarrow\mathrm{2}} \left({x}−\mathrm{2}\right){F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}={a}+{b}\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{5}}\:{so} \\ $$$${F}\left({x}\right)=\:\:\frac{\mathrm{1}}{\mathrm{5}\left({x}−\mathrm{2}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{5}}{x}\:+{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)=\frac{−\mathrm{1}}{\mathrm{10}}\:+{c}\:\Rightarrow\:{F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{5}\left({x}−\mathrm{2}\right)}\:−\frac{\mathrm{1}}{\mathrm{10}}\:\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\int_{\mathrm{3}} ^{\mathrm{4}} \:{F}\left({x}\right){dx}=\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\:\frac{{dx}}{\mathrm{5}\left({x}−\mathrm{2}\right)}\:−\frac{\mathrm{1}}{\mathrm{10}}\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{10}}\int_{\mathrm{3}} ^{\mathrm{4}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\left[{ln}\mid{x}−\mathrm{2}\mid\right]_{\mathrm{3}} ^{\mathrm{4}} \:\:−\frac{\mathrm{1}}{\mathrm{10}}\left[{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{3}} ^{\mathrm{4}} \:\:+\frac{\mathrm{1}}{\mathrm{10}}\:\left[{arctanx}\right]_{\mathrm{3}} ^{\mathrm{4}} \\ $$$$=\frac{{ln}\mathrm{2}}{\mathrm{5}}\:−\frac{\mathrm{1}}{\mathrm{10}}\left({ln}\left(\mathrm{17}\right)−{ln}\left(\mathrm{10}\right)\right)+\frac{\mathrm{1}}{\mathrm{10}}\left({arctan}\mathrm{4}−{arctam}\mathrm{3}\right). \\ $$
