Menu Close

find-3-x-2-x-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 27596 by abdo imad last updated on 10/Jan/18
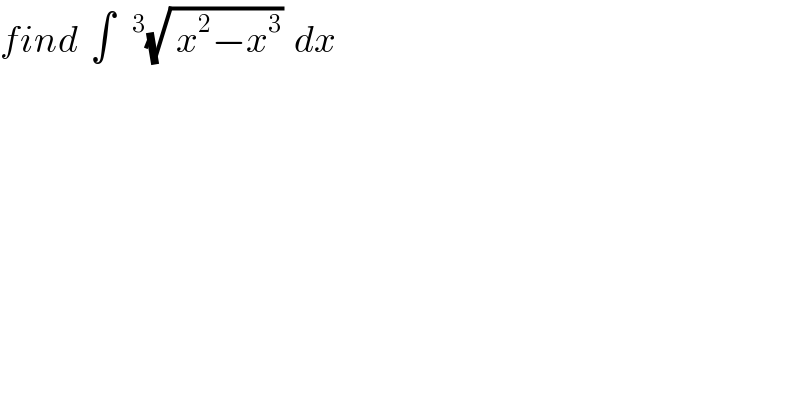
find ∫ ^3 (√( x^2 −x^3 )) dx
$${find}\:\:\int\:\:\:^{\mathrm{3}} \sqrt{\:{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }\:\:{dx} \\ $$
Commented by abdo imad last updated on 28/Jan/18
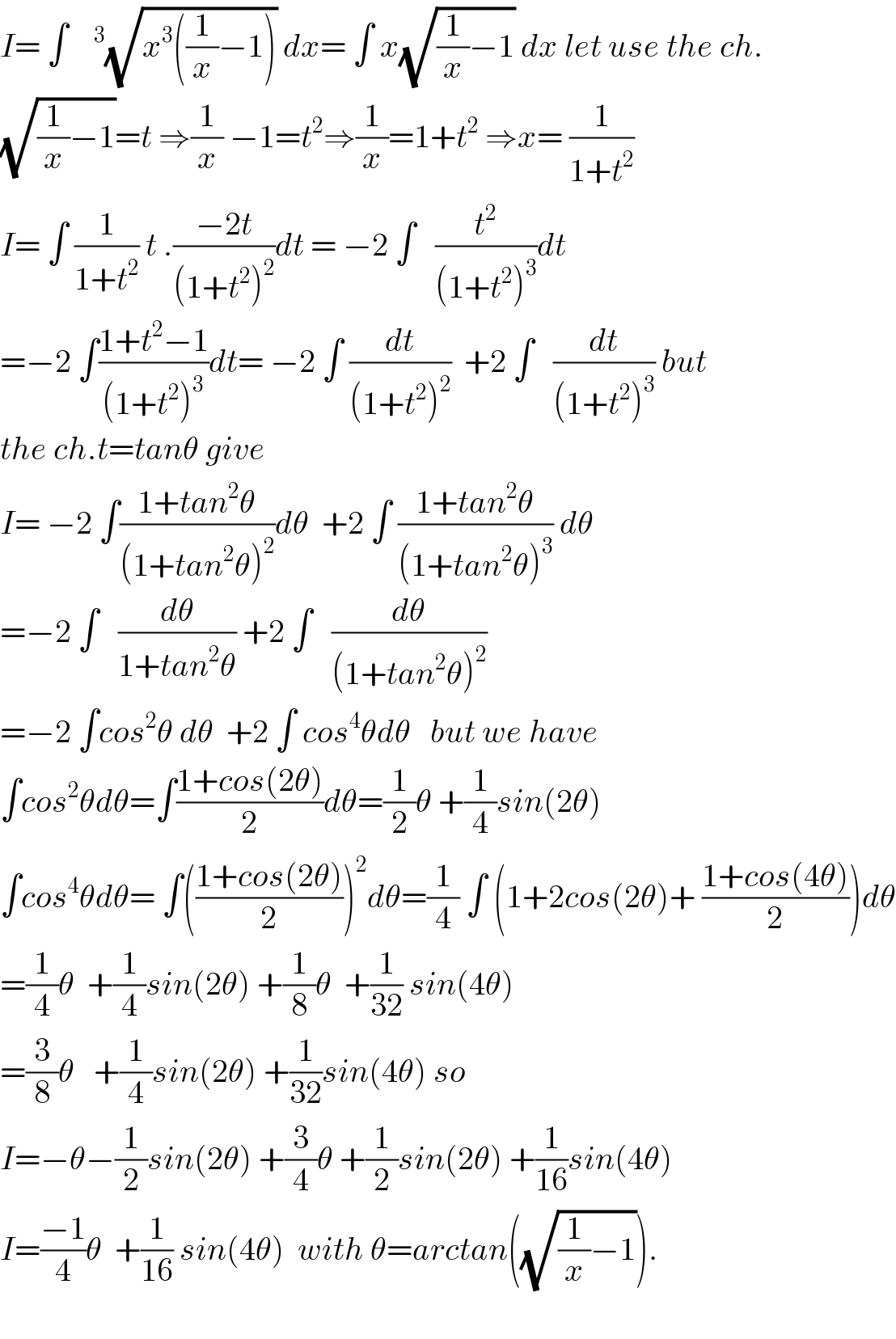
I= ∫ ^3 (√(x^3 ((1/x)−1))) dx= ∫ x(√((1/x)−1)) dx let use the ch. (√((1/x)−1))=t ⇒(1/x) −1=t^2 ⇒(1/x)=1+t^2 ⇒x= (1/(1+t^2 )) I= ∫ (1/(1+t^2 )) t .((−2t)/((1+t^2 )^2 ))dt = −2 ∫ (t^2 /((1+t^2 )^3 ))dt =−2 ∫((1+t^2 −1)/((1+t^2 )^3 ))dt= −2 ∫ (dt/((1+t^2 )^2 )) +2 ∫ (dt/((1+t^2 )^3 )) but the ch.t=tanθ give I= −2 ∫((1+tan^2 θ)/((1+tan^2 θ)^2 ))dθ +2 ∫ ((1+tan^2 θ)/((1+tan^2 θ)^3 )) dθ =−2 ∫ (dθ/(1+tan^2 θ)) +2 ∫ (dθ/((1+tan^2 θ)^2 )) =−2 ∫cos^2 θ dθ +2 ∫ cos^4 θdθ but we have ∫cos^2 θdθ=∫((1+cos(2θ))/2)dθ=(1/2)θ +(1/4)sin(2θ) ∫cos^4 θdθ= ∫(((1+cos(2θ))/2))^2 dθ=(1/4) ∫ (1+2cos(2θ)+ ((1+cos(4θ))/2))dθ =(1/4)θ +(1/4)sin(2θ) +(1/8)θ +(1/(32)) sin(4θ) =(3/8)θ +(1/4)sin(2θ) +(1/(32))sin(4θ) so I=−θ−(1/2)sin(2θ) +(3/4)θ +(1/2)sin(2θ) +(1/(16))sin(4θ) I=((−1)/4)θ +(1/(16)) sin(4θ) with θ=arctan((√((1/x)−1))).
$${I}=\:\int\:\:\:\:^{\mathrm{3}} \sqrt{{x}^{\mathrm{3}} \left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}\:{dx}=\:\int\:{x}\sqrt{\frac{\mathrm{1}}{{x}}−\mathrm{1}}\:{dx}\:{let}\:{use}\:{the}\:{ch}. \\ $$$$\sqrt{\frac{\mathrm{1}}{{x}}−\mathrm{1}}={t}\:\Rightarrow\frac{\mathrm{1}}{{x}}\:−\mathrm{1}={t}^{\mathrm{2}} \Rightarrow\frac{\mathrm{1}}{{x}}=\mathrm{1}+{t}^{\mathrm{2}} \:\Rightarrow{x}=\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}=\:\int\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{t}\:.\frac{−\mathrm{2}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:=\:−\mathrm{2}\:\int\:\:\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }{dt} \\ $$$$=−\mathrm{2}\:\int\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }{dt}=\:−\mathrm{2}\:\int\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:+\mathrm{2}\:\int\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }\:{but} \\ $$$${the}\:{ch}.{t}={tan}\theta\:{give} \\ $$$${I}=\:−\mathrm{2}\:\int\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta\:\:+\mathrm{2}\:\int\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{3}} }\:{d}\theta \\ $$$$=−\mathrm{2}\:\int\:\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:+\mathrm{2}\:\int\:\:\:\frac{{d}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{2}\:\int{cos}^{\mathrm{2}} \theta\:{d}\theta\:\:+\mathrm{2}\:\int\:{cos}^{\mathrm{4}} \theta{d}\theta\:\:\:{but}\:{we}\:{have} \\ $$$$\int{cos}^{\mathrm{2}} \theta{d}\theta=\int\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\theta\:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}\theta\right) \\ $$$$\int{cos}^{\mathrm{4}} \theta{d}\theta=\:\int\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\right)^{\mathrm{2}} {d}\theta=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}\theta\right)+\:\frac{\mathrm{1}+{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\theta\:\:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}\theta\right)\:+\frac{\mathrm{1}}{\mathrm{8}}\theta\:\:+\frac{\mathrm{1}}{\mathrm{32}}\:{sin}\left(\mathrm{4}\theta\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\theta\:\:\:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}\theta\right)\:+\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{4}\theta\right)\:{so} \\ $$$${I}=−\theta−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\:+\frac{\mathrm{3}}{\mathrm{4}}\theta\:+\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\:+\frac{\mathrm{1}}{\mathrm{16}}{sin}\left(\mathrm{4}\theta\right) \\ $$$${I}=\frac{−\mathrm{1}}{\mathrm{4}}\theta\:\:+\frac{\mathrm{1}}{\mathrm{16}}\:{sin}\left(\mathrm{4}\theta\right)\:\:{with}\:\theta={arctan}\left(\sqrt{\frac{\mathrm{1}}{{x}}−\mathrm{1}}\right). \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *