Question Number 106329 by 175mohamed last updated on 04/Aug/20

$${find}\:\int_{−\mathrm{5}} ^{\mathrm{5}} \left(\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\right){dx}\:\:{whithout}\:{using} \\ $$$${trigonometric}\:{compensation} \\ $$
Answered by Her_Majesty last updated on 04/Aug/20
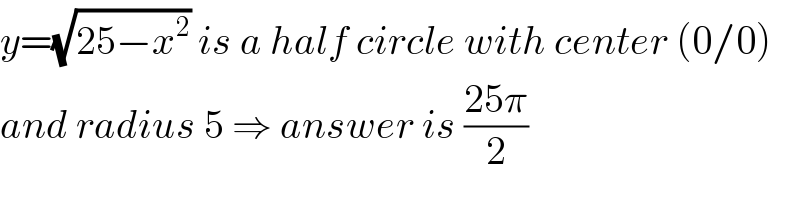
$${y}=\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\:{is}\:{a}\:{half}\:{circle}\:{with}\:{center}\:\left(\mathrm{0}/\mathrm{0}\right) \\ $$$${and}\:{radius}\:\mathrm{5}\:\Rightarrow\:{answer}\:{is}\:\frac{\mathrm{25}\pi}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Aug/20
![∫_(−5) ^5 (√(25−x^2 ))=2∫_0 ^5 (√(25−x^2 ))=2[(x/2)(√(25−x^2 ))+((25)/2)sin^(−1) (x/5)]_0 ^5 =((25π)/2)](https://www.tinkutara.com/question/Q106332.png)
$$\int_{−\mathrm{5}} ^{\mathrm{5}} \sqrt{\mathrm{25}−{x}^{\mathrm{2}} }=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{5}} \sqrt{\mathrm{25}−{x}^{\mathrm{2}} }=\mathrm{2}\left[\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\frac{\mathrm{25}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{x}}{\mathrm{5}}\right]_{\mathrm{0}} ^{\mathrm{5}} \\ $$$$=\frac{\mathrm{25}\pi}{\mathrm{2}} \\ $$
