Menu Close

find-5-6-7sin-2-if-tan-0-2-

Tinku Tara 0 Comments
Pin




Question Number 112136 by weltr last updated on 06/Sep/20
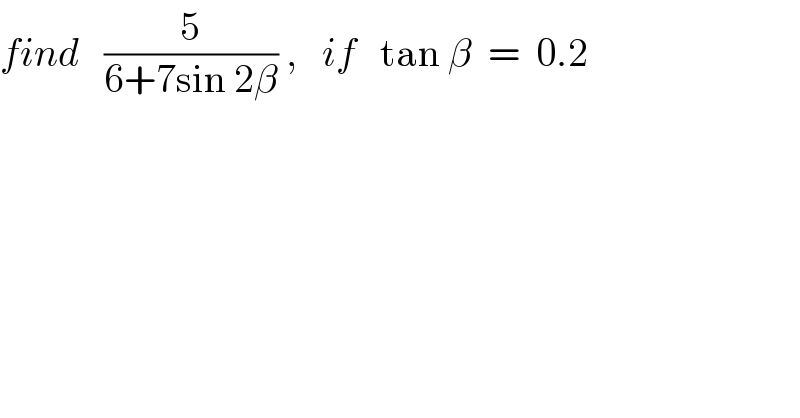
find (5/(6+7sin 2β)) , if tan β = 0.2
$${find}\:\:\:\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7sin}\:\mathrm{2}\beta}\:,\:\:\:{if}\:\:\:\mathrm{tan}\:\beta\:\:=\:\:\mathrm{0}.\mathrm{2} \\ $$
Answered by bemath last updated on 06/Sep/20
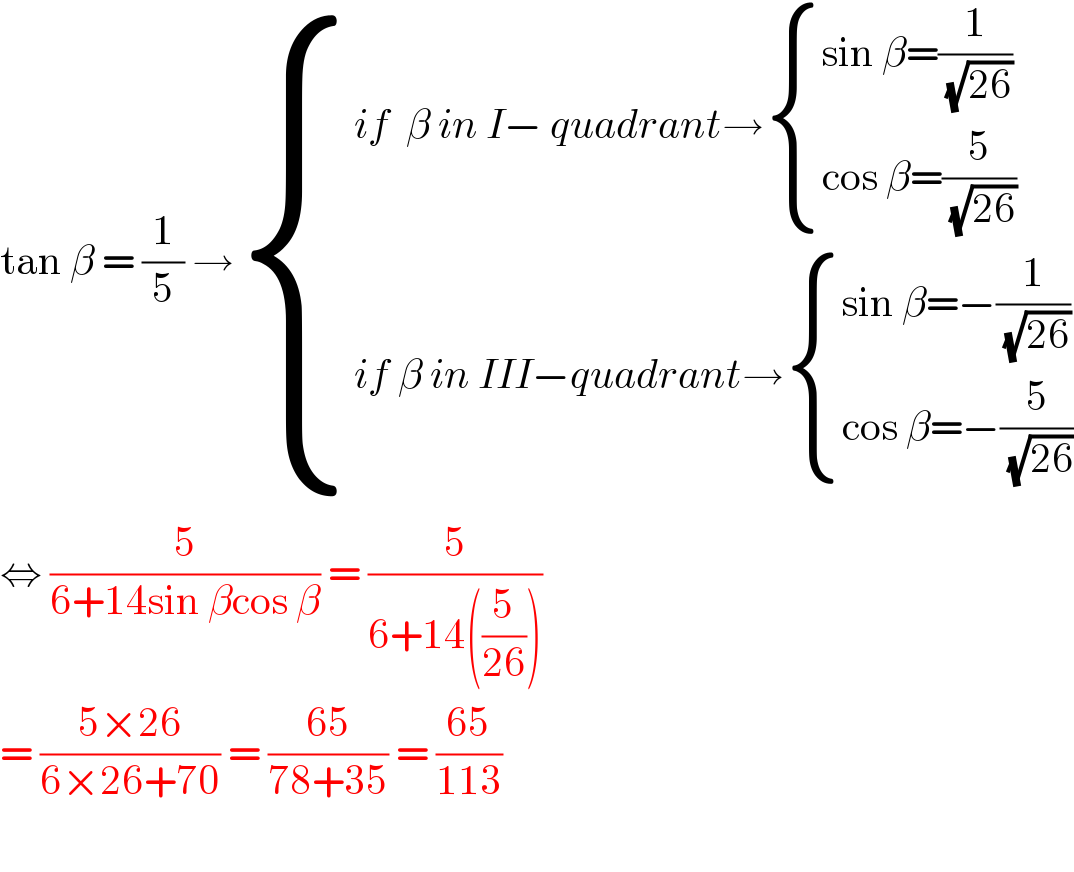
tan β = (1/5) → { ((if β in I− quadrant→ { ((sin β=(1/( (√(26)))))),((cos β=(5/( (√(26)))))) :})),((if β in III−quadrant→ { ((sin β=−(1/( (√(26)))))),((cos β=−(5/( (√(26)))))) :})) :} ⇔ (5/(6+14sin βcos β)) = (5/(6+14((5/(26))))) = ((5×26)/(6×26+70)) = ((65)/(78+35)) = ((65)/(113))
$$\mathrm{tan}\:\beta\:=\:\frac{\mathrm{1}}{\mathrm{5}}\:\rightarrow\begin{cases}{{if}\:\:\beta\:{in}\:{I}−\:{quadrant}\rightarrow\begin{cases}{\mathrm{sin}\:\beta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{26}}}}\\{\mathrm{cos}\:\beta=\frac{\mathrm{5}}{\:\sqrt{\mathrm{26}}}}\end{cases}}\\{{if}\:\beta\:{in}\:{III}−{quadrant}\rightarrow\begin{cases}{\mathrm{sin}\:\beta=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{26}}}}\\{\mathrm{cos}\:\beta=−\frac{\mathrm{5}}{\:\sqrt{\mathrm{26}}}}\end{cases}}\end{cases} \\ $$$$\Leftrightarrow\:\frac{\mathrm{5}}{\mathrm{6}+\mathrm{14sin}\:\beta\mathrm{cos}\:\beta}\:=\:\frac{\mathrm{5}}{\mathrm{6}+\mathrm{14}\left(\frac{\mathrm{5}}{\mathrm{26}}\right)} \\ $$$$=\:\frac{\mathrm{5}×\mathrm{26}}{\mathrm{6}×\mathrm{26}+\mathrm{70}}\:=\:\frac{\mathrm{65}}{\mathrm{78}+\mathrm{35}}\:=\:\frac{\mathrm{65}}{\mathrm{113}} \\ $$$$ \\ $$
Commented by weltr last updated on 06/Sep/20
thanks
$${thanks} \\ $$
Answered by $@y@m last updated on 06/Sep/20
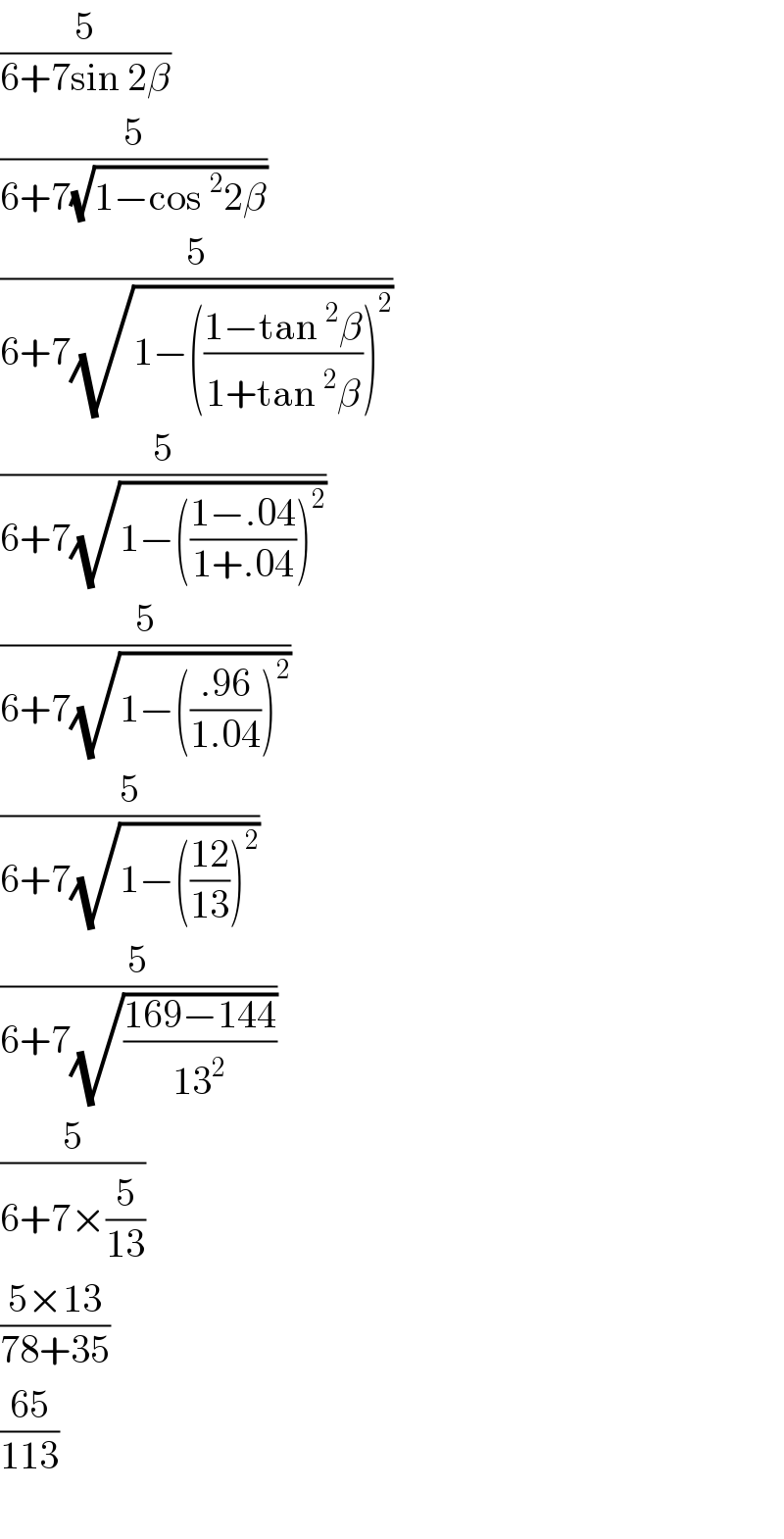
(5/(6+7sin 2β)) (5/(6+7(√(1−cos^2 2β)))) (5/(6+7(√(1−(((1−tan^2 β)/(1+tan^2 β)))^2 )))) (5/(6+7(√(1−(((1−.04)/(1+.04)))^2 )))) (5/(6+7(√(1−(((.96)/(1.04)))^2 )))) (5/(6+7(√(1−(((12)/(13)))^2 )))) (5/(6+7(√((169−144)/(13^2 ))))) (5/(6+7×(5/(13)))) ((5×13)/(78+35)) ((65)/(113))
$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7sin}\:\mathrm{2}\beta} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7}\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\beta}} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7}\sqrt{\mathrm{1}−\left(\frac{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \beta}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \beta}\right)^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7}\sqrt{\mathrm{1}−\left(\frac{\mathrm{1}−.\mathrm{04}}{\mathrm{1}+.\mathrm{04}}\right)^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7}\sqrt{\mathrm{1}−\left(\frac{.\mathrm{96}}{\mathrm{1}.\mathrm{04}}\right)^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7}\sqrt{\mathrm{1}−\left(\frac{\mathrm{12}}{\mathrm{13}}\right)^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7}\sqrt{\frac{\mathrm{169}−\mathrm{144}}{\mathrm{13}^{\mathrm{2}} }}} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}+\mathrm{7}×\frac{\mathrm{5}}{\mathrm{13}}} \\ $$$$\frac{\mathrm{5}×\mathrm{13}}{\mathrm{78}+\mathrm{35}} \\ $$$$\frac{\mathrm{65}}{\mathrm{113}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *