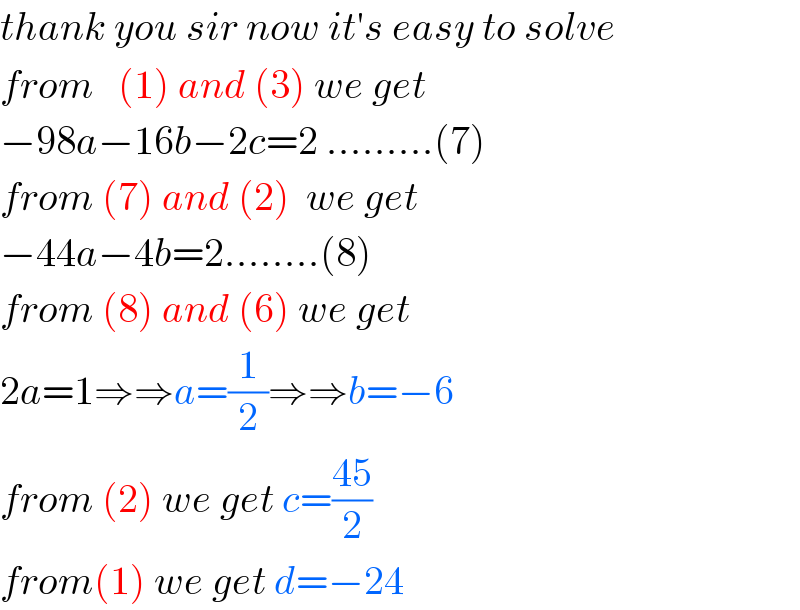find-a-b-c-d-if-f-x-ax-3-bx-2-cx-d-3-3-is-maximum-value-5-1-is-minimum-value-4-2-is-inflection-point-

Question Number 92277 by M±th+et+s last updated on 05/May/20

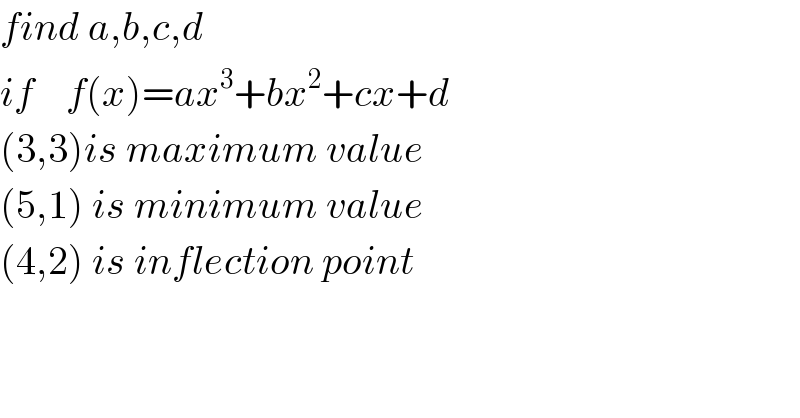
f i n d a, b, c, d

i f f (x) = {a x}^{3} + {b x}^{2} + c x + d

(3, 3) i s m a x i m u m v a l u e

(5, 1) i s m i n i m u m v a l u e

(4, 2) i s i n f l e c t i o n p o i n t

Commented by M±th+et+s last updated on 06/May/20

t h a n k y o u s i r b u t i f w e p u t x = 3

f (3) = \frac{27}{3} - 4 (9) + 15 (3) - \frac{46}{3}

f (3) = 18 - \frac{46}{3} = \frac{8}{3}

b u t i n t h e q u e s t i o n f (3) = 3 ? ?

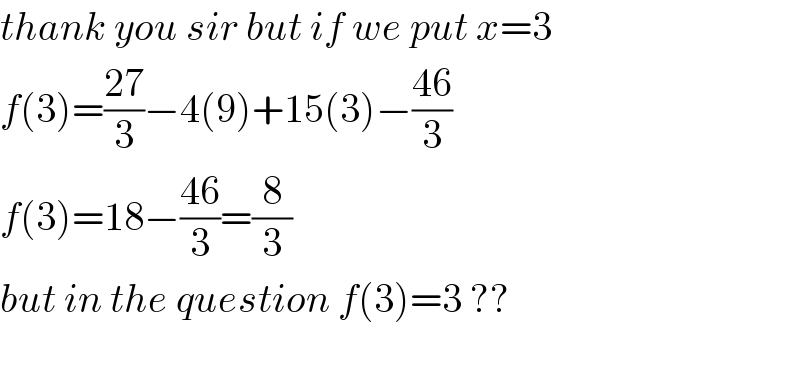
Commented by john santu last updated on 06/May/20

it does mean question inconsistent

f^{'} (x) = {3 ax}^{2} + 2 bx + c = 0

has roots x = 5 & x = 3

3 a (x - 5) (x - 3) \equiv {3 ax}^{2} + 2 bx + c

3 a (x^{2} - 8 x + 15) \equiv {3 ax}^{2} + 2 bx + c

2 b = - 24 a \Rightarrow b = - 12 a

c = 45 a

f (x) = {ax}^{3} - {12 ax}^{2} + 45 a + d

(3, 3) \Rightarrow 3 = 27 a - 108 a + 135 a + d

(4, 2) \Rightarrow 2 = 64 a - 192 a + 90 a + d

Commented by M±th+et+s last updated on 06/May/20

i t h i n k t h e r i g h t s o l u t i o n i s

a = \frac{1}{2} b = - 6 c = \frac{45}{2} d = - 24

f (x) = \frac{1}{2} x^{3} - 6 x^{2} + \frac{45}{2} x - 24

f (3) = \frac{27}{2} - 54 + \frac{45}{2} (3) - 24 = 3

f (5) = \frac{125}{2} - 150 + \frac{225}{2} - 24 = 1

f (4) = 32 - 96 + 90 - 24 = 2

f^{'} (x) = \frac{3}{2} x^{2} - 12 x + \frac{45}{2}

f^{'} (x) = 0 x_{1} = 3, x_{2} = 5

f^{″} (x) = 3 x - 12

f^{″} (x) = 0 x = 4

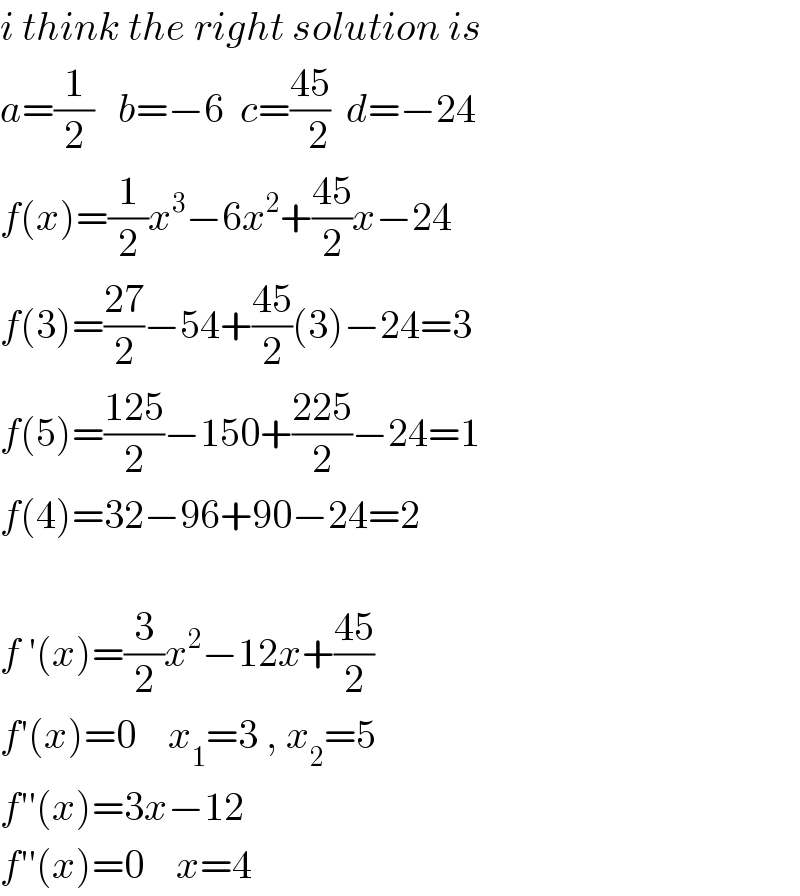
Commented by john santu last updated on 06/May/20

just two equations are enough. ��

Answered by MJS last updated on 06/May/20

{a x}^{3} + {b x}^{2} + c x + d = y

3 {a x}^{2} + 2 b x + c = y^{'}

6 a x + 2 b = y^{″}

(3, 3) \in f (x)

27 a + 9 b + 3 c + d = 3 (I)

(3, 3) \max

27 a + 6 b + c = 0 (I I)

(5, 1) \in f (x)

125 a + 25 b b + 5 c + d = 1 (I I I)

(5, 1) \min

75 a + 10 b + c = 0 (I V)

(4, 2) \in f (x)

64 a + 16 b + 4 c + d = 2 (V)

(4, 2) inflection

24 a + 2 b = 0 (V I)

6 equations and only 4 unknowns

too much info might be inconsistent

but in this case solving the system leads to

a = \frac{1}{2}, b = - 6, c = \frac{45}{2}, d = - 24

Commented by MJS last updated on 06/May/20

yes . we need only 4 equations to solve . if we

have more we must check if they fit together

Commented by M±th+et+s last updated on 06/May/20

t h a n k y o u s i r n o w {i t}^{'} s e a s y t o s o l v e

f r o m (1) a n d (3) w e g e t

- 98 a - 16 b - 2 c = 2 \dots \dots \dots (7)

f r o m (7) a n d (2) w e g e t

- 44 a - 4 b = 2 \dots \dots . . (8)

f r o m (8) a n d (6) w e g e t

2 a = 1 \Rightarrow\Rightarrow a = \frac{1}{2} \Rightarrow\Rightarrow b = - 6

f r o m (2) w e g e t c = \frac{45}{2}

f r o m (1) w e g e t d = - 24