Question Number 182216 by Acem last updated on 05/Dec/22
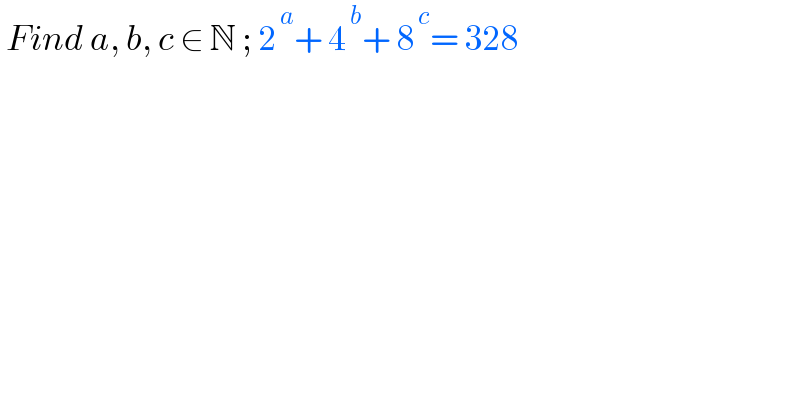
$$\:{Find}\:{a},\:{b},\:{c}\:\in\:\mathbb{N}\:;\:\mathrm{2}^{\:{a}} +\:\mathrm{4}^{\:{b}} +\:\mathrm{8}^{\:{c}} =\:\mathrm{328} \\ $$
Commented by SANOGO last updated on 06/Dec/22
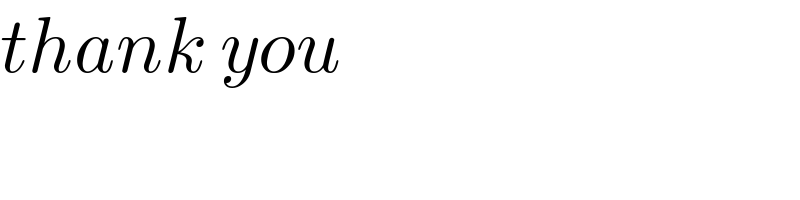
$${thank}\:{you} \\ $$
Commented by Acem last updated on 06/Dec/22

$$\:{You}'{re}\:{very}\:{much}\:{welcome}\:{Mr}.\:{Sanogo} \\ $$$$\:{you}\:{can}\:{see}\:{the}\:{way}\:{to}\:{find}\:{the}\:{powers}\:{below} \\ $$$$\:{especialy}\:{if}\:{the}\:\mathrm{2}{nd}\:{side}\:{was}\:{bigger}\:{than}\:\mathrm{328} \\ $$
Answered by HeferH last updated on 06/Dec/22

$$\:{Reminded}\:{me}\:{of}\:{the}\:{binary}\:{system}: \\ $$$$\:\mathrm{328}\:=\:\mathrm{2}^{\mathrm{8}} \:+\:\mathrm{2}^{\mathrm{6}\:} \:+\:\mathrm{2}^{\mathrm{3}} \:=\:\mathrm{256}\:+\:\mathrm{64}\:+\:\mathrm{8} \\ $$$$\:\mathrm{2}^{{a}} \:+\:\mathrm{2}^{\mathrm{2}{b}} \:+\:\mathrm{2}^{\mathrm{3}{c}} \:=\:\mathrm{2}^{\mathrm{8}} +\mathrm{2}^{\mathrm{6}} +\mathrm{2}^{\mathrm{3}} \\ $$$$\:{One}\:{solution}\:{would}\:{be}: \\ $$$$\:{a}\:=\:\mathrm{8},\:{b}\:=\:\mathrm{3},\:{c}\:=\:\mathrm{1}; \\ $$$$\:{Another}\:{one}: \\ $$$$\:{a}\:=\:\mathrm{3},\:{b}\:=\:\mathrm{4},\:{c}\:=\:\mathrm{2}; \\ $$$$\:{and}\:{another}\:{one}: \\ $$$$\:{a}\:=\:\mathrm{6}\:,\:{b}\:=\:\mathrm{8},\:{c}\:=\:\mathrm{1} \\ $$$$\:\begin{array}{|c|c|c|c|c|c|c|}{{a}}&\hline{\mathrm{2}{b}}&\hline{\mathrm{3}{c}}\\{\mathrm{8}}&\hline{\mathrm{6}}&\hline{\mathrm{3}}\\{\mathrm{3}}&\hline{\mathrm{6}}&\hline{\mathrm{8}}\\{\mathrm{6}}&\hline{\mathrm{3}}&\hline{\mathrm{8}}\\{\mathrm{8}}&\hline{\mathrm{3}}&\hline{\mathrm{3}}\\{\mathrm{6}}&\hline{\mathrm{8}}&\hline{\mathrm{3}}\\{\mathrm{3}}&\hline{\mathrm{8}}&\hline{\mathrm{6}}\\\hline\end{array} \\ $$$$\:\:{Since}\:{a},\:{b},\:{c}\:\in\:\mathbb{N}\: \\ $$
Commented by Acem last updated on 06/Dec/22
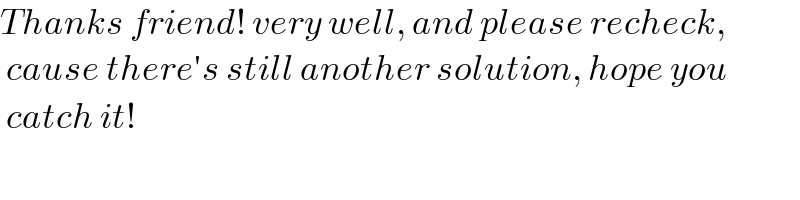
$${Thanks}\:{friend}!\:{very}\:{well},\:{and}\:{please}\:{recheck},\: \\ $$$$\:{cause}\:{there}'{s}\:{still}\:{another}\:{solution},\:{hope}\:{you} \\ $$$$\:{catch}\:{it}! \\ $$
Commented by Acem last updated on 06/Dec/22
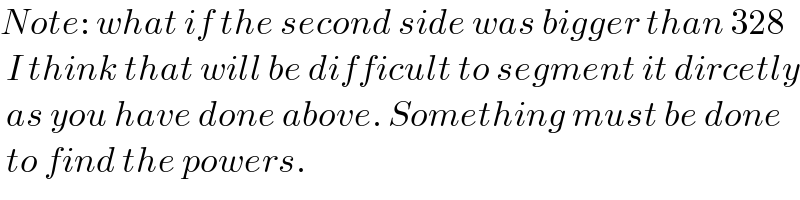
$${Note}:\:{what}\:{if}\:{the}\:{second}\:{side}\:{was}\:{bigger}\:{than}\:\mathrm{328} \\ $$$$\:{I}\:{think}\:{that}\:{will}\:{be}\:{difficult}\:{to}\:{segment}\:{it}\:{dircetly} \\ $$$$\:{as}\:{you}\:{have}\:{done}\:{above}.\:{Something}\:{must}\:{be}\:{done} \\ $$$$\:{to}\:{find}\:{the}\:{powers}. \\ $$
Commented by HeferH last updated on 06/Dec/22
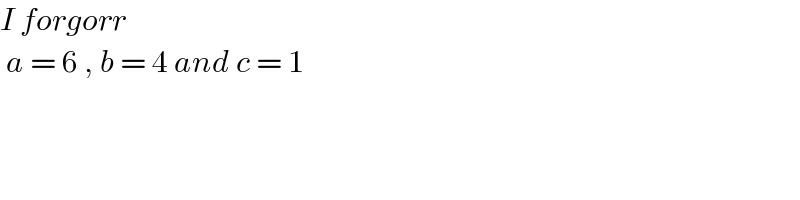
$${I}\:{forgorr} \\ $$$$\:{a}\:=\:\mathrm{6}\:,\:{b}\:=\:\mathrm{4}\:{and}\:{c}\:=\:\mathrm{1} \\ $$$$\: \\ $$
Commented by Acem last updated on 06/Dec/22

$${Yes}\:{Sir}!\:{Thanksss} \\ $$
Commented by Acem last updated on 06/Dec/22

$$\:{Hi}\:{Sir}!\:{Here}\:{it}\:{is}\:{the}\:{way}\:{to}\:{find}\:{the}\:{powers},\:{it}'{s} \\ $$$$\:{below}.\:{Thank}\:{you}\:{again}! \\ $$
Answered by Rasheed.Sindhi last updated on 06/Dec/22
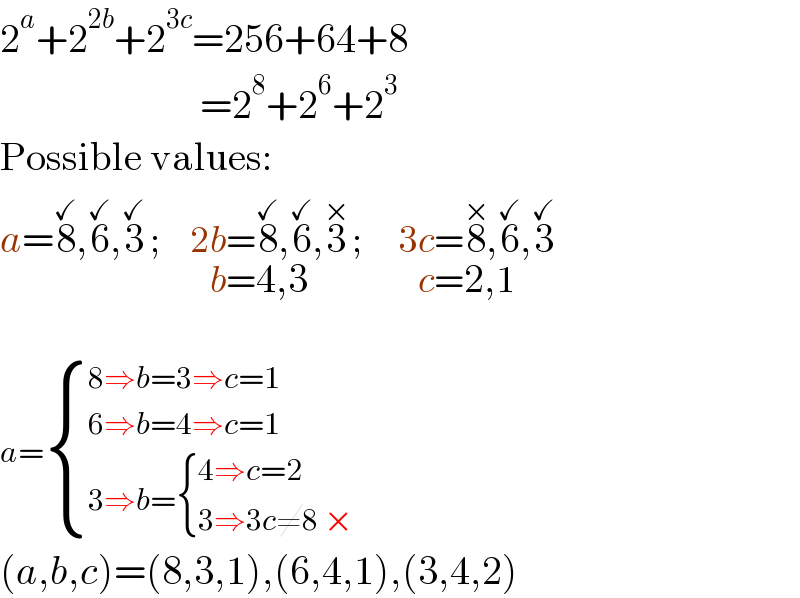
$$\mathrm{2}^{{a}} +\mathrm{2}^{\mathrm{2}{b}} +\mathrm{2}^{\mathrm{3}{c}} =\mathrm{256}+\mathrm{64}+\mathrm{8}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{8}} +\mathrm{2}^{\mathrm{6}} +\mathrm{2}^{\mathrm{3}} \\ $$$$\mathrm{Possible}\:\mathrm{values}: \\ $$$${a}=\overset{\checkmark} {\mathrm{8}},\overset{\checkmark} {\mathrm{6}},\overset{\checkmark} {\mathrm{3}}\:;\:\:\:\:\:\mathrm{2}\underset{{b}=\mathrm{4},\mathrm{3}} {{b}=\mathrm{8},\mathrm{6}},\overset{×} {\mathrm{3}}\:;\:\:\:\:\:\:\mathrm{3}\underset{{c}=\mathrm{2},\mathrm{1}} {{c}=\mathrm{8},\mathrm{6}},\overset{\checkmark} {\mathrm{3}} \\ $$$$ \\ $$$${a}=\begin{cases}{\mathrm{8}\Rightarrow{b}=\mathrm{3}\Rightarrow{c}=\mathrm{1}}\\{\mathrm{6}\Rightarrow{b}=\mathrm{4}\Rightarrow{c}=\mathrm{1}}\\{\mathrm{3}\Rightarrow{b}=\begin{cases}{\mathrm{4}\Rightarrow{c}=\mathrm{2}}\\{\mathrm{3}\Rightarrow\mathrm{3}{c}\neq\mathrm{8}\:×}\end{cases}}\end{cases}\: \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{8},\mathrm{3},\mathrm{1}\right),\left(\mathrm{6},\mathrm{4},\mathrm{1}\right),\left(\mathrm{3},\mathrm{4},\mathrm{2}\right) \\ $$
Commented by Acem last updated on 06/Dec/22

$${Thanks}\:{Sir}! \\ $$
Answered by Acem last updated on 06/Dec/22

