Menu Close

find-a-equivalent-of-A-n-0-n-1-1-x-n-n-dx-n-

Tinku Tara 0 Comments
Pin




Question Number 33340 by prof Abdo imad last updated on 14/Apr/18
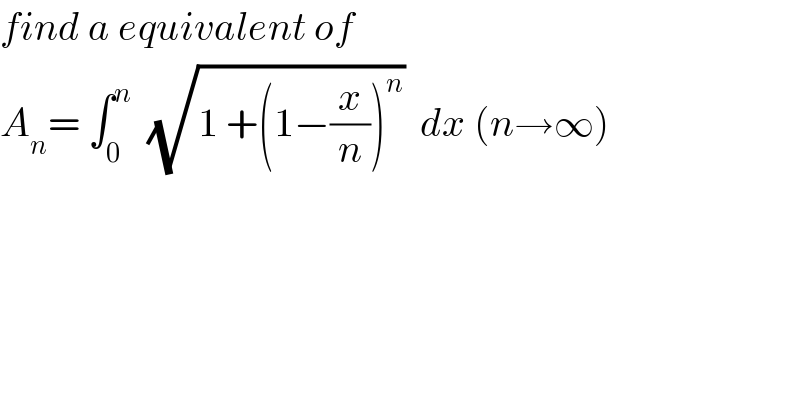
find a equivalent of A_n = ∫_0 ^n (√(1 +(1−(x/n))^n )) dx (n→∞)
$${find}\:{a}\:{equivalent}\:{of} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{{n}} \:\:\sqrt{\mathrm{1}\:+\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} }\:\:{dx}\:\left({n}\rightarrow\infty\right) \\ $$
Commented by prof Abdo imad last updated on 25/Apr/18
we know that (1+u)^α =1+αu +((α(α−1))/2) α^2 +o(α^3 ) (1−(x/n))^n = 1−x+ ((n(n−1))/2) (x^2 /n^2 ) +o( (x^3 /n^3 )) ⇒ 1+(1−(x/n))^n ∼ 2 −x+ ((n(n−1)x^2 )/(2n^2 )) (n→+∞)and (√(2−x +((n(n−1))/(2n^2 ))x^2 )) =(√(2( 1−(x/2) +((n(n−1)x^2 )/(4n^2 )))) ∼(√2)(1−(1/2)( (x/2) −((n(n−1)x^2 )/(4n^2 )))) =(√2) −((√2)/4) x +((√2)/8) ((n(n−1)x^2 )/n^2 ) ⇒ A_n ∼ ∫_0 ^n ((√2) −((√2)/4) x +((√2)/8) ((n(n−1)x^2 )/n^2 ))dx ⇒ A_n ∼ n(√2) −((√2)/8) n^2 +((√2)/(24)) ((n(n−1)n^3 )/n^2 ) ⇒ A_n ∼n(√2) −((√2)/8) n^2 +((√2)/(24)) n^2 (n−1) (n→+∞)
$${we}\:{know}\:{that}\:\left(\mathrm{1}+{u}\right)^{\alpha} \:=\mathrm{1}+\alpha{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}}\:\alpha^{\mathrm{2}} \:+{o}\left(\alpha^{\mathrm{3}} \right) \\ $$$$\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} \:=\:\mathrm{1}−{x}+\:\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\:\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\:+{o}\left(\:\frac{{x}^{\mathrm{3}} }{{n}^{\mathrm{3}} }\right)\:\Rightarrow \\ $$$$\mathrm{1}+\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} \:\sim\:\:\mathrm{2}\:\:−{x}+\:\frac{{n}\left({n}−\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{2}} }\:\left({n}\rightarrow+\infty\right){and} \\ $$$$\sqrt{\mathrm{2}−{x}\:+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }{x}^{\mathrm{2}} }\:\:=\sqrt{\mathrm{2}\left(\:\mathrm{1}−\frac{{x}}{\mathrm{2}}\:+\frac{{n}\left({n}−\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{4}{n}^{\mathrm{2}} }\right.} \\ $$$$\sim\sqrt{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\:\:\frac{{x}}{\mathrm{2}}\:−\frac{{n}\left({n}−\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{4}{n}^{\mathrm{2}} }\right)\right) \\ $$$$=\sqrt{\mathrm{2}}\:\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:{x}\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\frac{{n}\left({n}−\mathrm{1}\right){x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\:\:\Rightarrow \\ $$$${A}_{{n}} \:\:\sim\:\:\int_{\mathrm{0}} ^{{n}} \left(\sqrt{\mathrm{2}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:{x}\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\frac{{n}\left({n}−\mathrm{1}\right){x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right){dx}\:\Rightarrow \\ $$$${A}_{{n}} \:\:\sim\:{n}\sqrt{\mathrm{2}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:{n}^{\mathrm{2}} \:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\:\frac{{n}\left({n}−\mathrm{1}\right){n}^{\mathrm{3}} }{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$${A}_{{n}} \:\:\sim{n}\sqrt{\mathrm{2}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:{n}^{\mathrm{2}} \:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\:{n}^{\mathrm{2}} \left({n}−\mathrm{1}\right)\:\:\left({n}\rightarrow+\infty\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *