Menu Close

find-A-n-0-pi-4-cosx-sinx-n-dx-

Tinku Tara 0 Comments
Pin




Question Number 36762 by abdo.msup.com last updated on 05/Jun/18
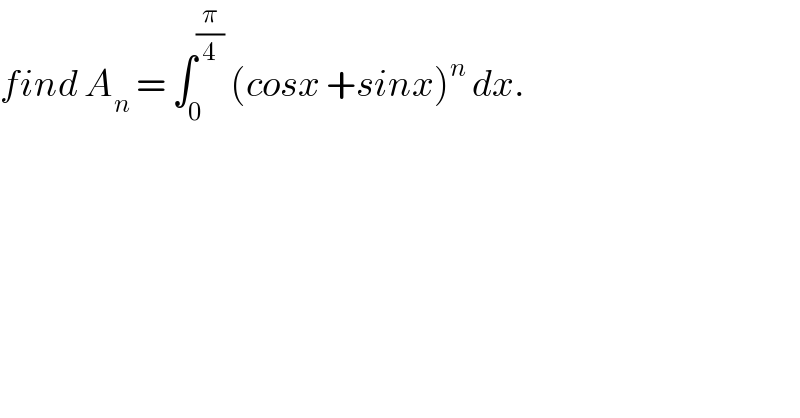
find A_n = ∫_0 ^(π/4) (cosx +sinx)^n dx.
$${find}\:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left({cosx}\:+{sinx}\right)^{{n}} \:{dx}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
Commented by abdo.msup.com last updated on 05/Jun/18
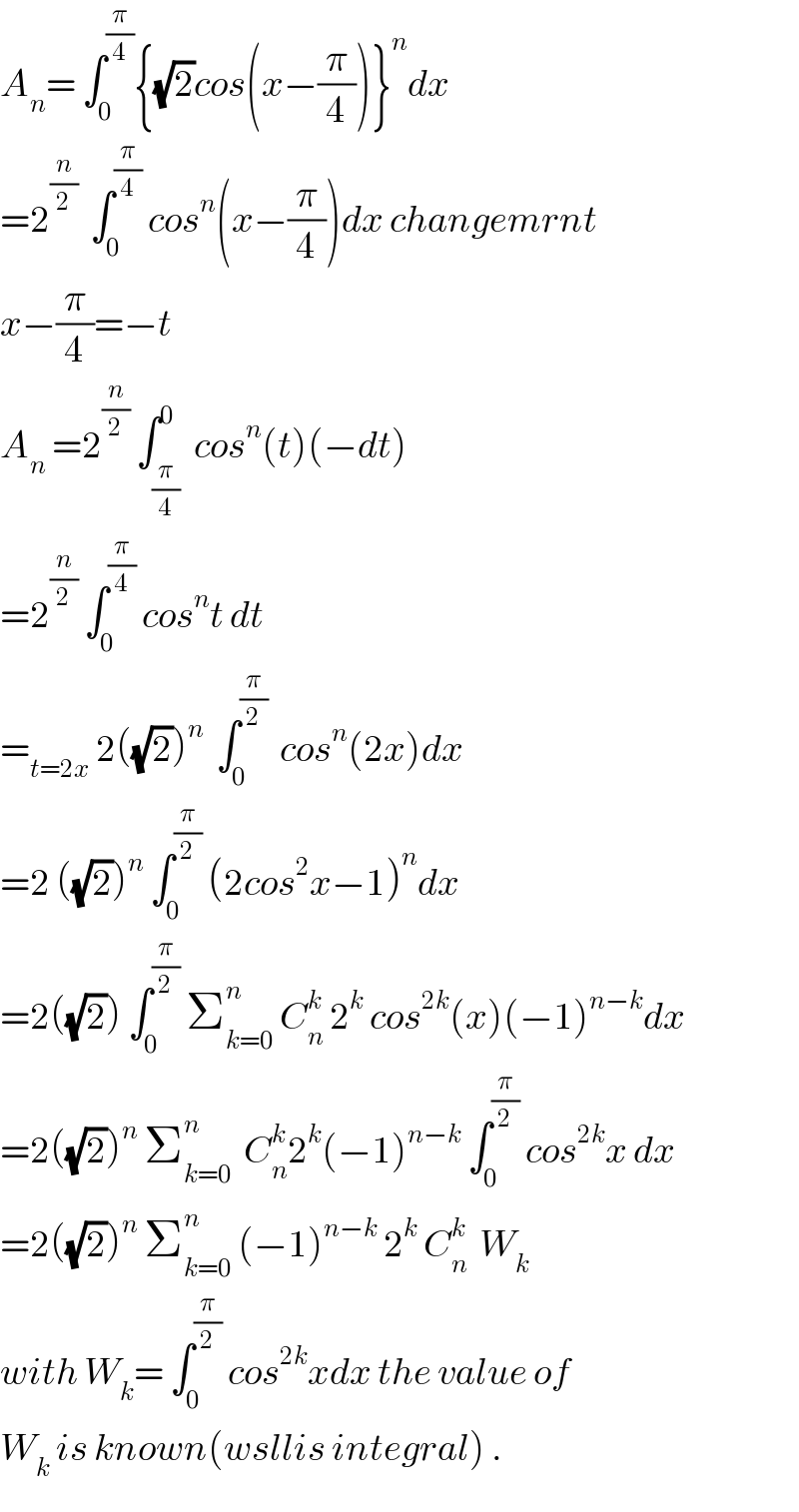
A_n = ∫_0 ^(π/4) {(√2)cos(x−(π/4))}^n dx =2^(n/2) ∫_0 ^(π/4) cos^n (x−(π/4))dx changemrnt x−(π/4)=−t A_n =2^(n/2) ∫_(π/4) ^0 cos^n (t)(−dt) =2^(n/2) ∫_0 ^(π/4) cos^n t dt =_(t=2x) 2((√2))^n ∫_0 ^(π/2) cos^n (2x)dx =2 ((√2))^n ∫_0 ^(π/2) (2cos^2 x−1)^n dx =2((√2)) ∫_0 ^(π/2) Σ_(k=0) ^n C_n ^k 2^k cos^(2k) (x)(−1)^(n−k) dx =2((√2))^n Σ_(k=0) ^n C_n ^k 2^k (−1)^(n−k) ∫_0 ^(π/2) cos^(2k) x dx =2((√2))^n Σ_(k=0) ^n (−1)^(n−k) 2^k C_n ^k W_k with W_k = ∫_0 ^(π/2) cos^(2k) xdx the value of W_k is known(wsllis integral) .
$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right\}^{{n}} {dx} \\ $$$$=\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{{n}} \left({x}−\frac{\pi}{\mathrm{4}}\right){dx}\:{changemrnt} \\ $$$${x}−\frac{\pi}{\mathrm{4}}=−{t} \\ $$$${A}_{{n}} \:=\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \:\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{0}} \:{cos}^{{n}} \left({t}\right)\left(−{dt}\right) \\ $$$$=\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{{n}} {t}\:{dt} \\ $$$$=_{{t}=\mathrm{2}{x}} \:\mathrm{2}\left(\sqrt{\mathrm{2}}\right)^{{n}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cos}^{{n}} \left(\mathrm{2}{x}\right){dx} \\ $$$$=\mathrm{2}\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}\right)^{{n}} {dx} \\ $$$$=\mathrm{2}\left(\sqrt{\mathrm{2}}\right)\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\mathrm{2}^{{k}} \:{cos}^{\mathrm{2}{k}} \left({x}\right)\left(−\mathrm{1}\right)^{{n}−{k}} {dx} \\ $$$$=\mathrm{2}\left(\sqrt{\mathrm{2}}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \mathrm{2}^{{k}} \left(−\mathrm{1}\right)^{{n}−{k}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{k}} {x}\:{dx} \\ $$$$=\mathrm{2}\left(\sqrt{\mathrm{2}}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{n}−{k}} \:\mathrm{2}^{{k}} \:{C}_{{n}} ^{{k}} \:\:{W}_{{k}} \\ $$$${with}\:{W}_{{k}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{k}} {xdx}\:{the}\:{value}\:{of} \\ $$$${W}_{{k}} \:{is}\:{known}\left({wsllis}\:{integral}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
A_n =∫_0 ^(Π/4) {(√2) ((1/( (√2)))cosx+(1/( (√2) ))sinx)}^n dx A_n =∫_0 ^(Π/4) 2^(n/2) ×sin^n ((Π/4)+x)dx t=(Π/4)+x dt=dx A_n =2^(n/2) ∫_(Π/4) ^(Π/2) sin^n tdt I_n =∫sin^n tdt use reduction formula contd
$${A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \left\{\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cosx}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}{sinx}\right)\right\}^{{n}} {dx} \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \mathrm{2}^{\frac{{n}}{\mathrm{2}}} ×{sin}^{{n}} \left(\frac{\Pi}{\mathrm{4}}+{x}\right){dx} \\ $$$${t}=\frac{\Pi}{\mathrm{4}}+{x} \\ $$$${dt}={dx} \\ $$$${A}_{{n}} =\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \int_{\frac{\Pi}{\mathrm{4}}} ^{\frac{\Pi}{\mathrm{2}}} {sin}^{{n}} {tdt} \\ $$$${I}_{{n}} =\int{sin}^{{n}} {tdt}\:\:\:{use}\:{reduction}\:{formula} \\ $$$${contd} \\ $$$$\: \\ $$$$ \\ $$$$\:\: \\ $$
Commented by NECx last updated on 05/Jun/18
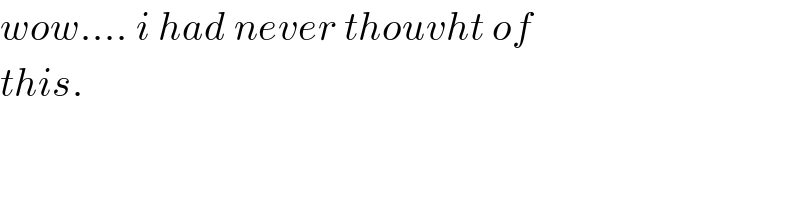
wow.... i had never thouvht of this.
$${wow}….\:{i}\:{had}\:{never}\:{thouvht}\:{of} \\ $$$${this}. \\ $$
Commented by MJS last updated on 05/Jun/18
the method is ok but something seems not clear to me. it should be: for n=2k A_0 =(π/4); A_(k+1) =((2k−1)/k)A_k +(1/(2k)) for n=2k+1 A_1 =1; A_(k+1) =((4k)/(2k+1))A_k +(1/(2k+1)) ⇒ A_0 =(π/4); A_1 =1; A_(n+2) =2((n−1)/n)A_n +(1/n) please correct me if I′m wrong
$$\mathrm{the}\:\mathrm{method}\:\mathrm{is}\:\mathrm{ok}\:\mathrm{but}\:\mathrm{something}\:\mathrm{seems}\:\mathrm{not} \\ $$$$\mathrm{clear}\:\mathrm{to}\:\mathrm{me}.\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}: \\ $$$$ \\ $$$$\mathrm{for}\:{n}=\mathrm{2}{k} \\ $$$${A}_{\mathrm{0}} =\frac{\pi}{\mathrm{4}};\:{A}_{{k}+\mathrm{1}} =\frac{\mathrm{2}{k}−\mathrm{1}}{{k}}{A}_{{k}} +\frac{\mathrm{1}}{\mathrm{2}{k}} \\ $$$$\mathrm{for}\:{n}=\mathrm{2}{k}+\mathrm{1} \\ $$$${A}_{\mathrm{1}} =\mathrm{1};\:{A}_{{k}+\mathrm{1}} =\frac{\mathrm{4}{k}}{\mathrm{2}{k}+\mathrm{1}}{A}_{{k}} +\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$ \\ $$$$\Rightarrow\:{A}_{\mathrm{0}} =\frac{\pi}{\mathrm{4}};\:{A}_{\mathrm{1}} =\mathrm{1};\:{A}_{{n}+\mathrm{2}} =\mathrm{2}\frac{{n}−\mathrm{1}}{{n}}{A}_{{n}} +\frac{\mathrm{1}}{{n}} \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{correct}\:\mathrm{me}\:\mathrm{if}\:\mathrm{I}'\mathrm{m}\:\mathrm{wrong} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
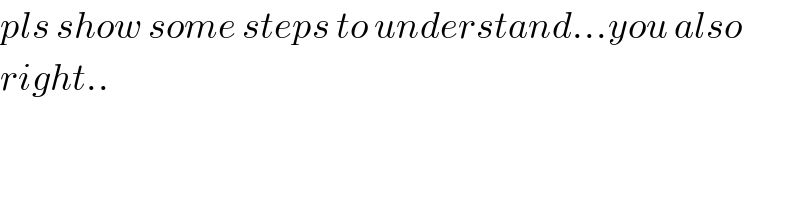
pls show some steps to understand...you also right..
$${pls}\:{show}\:{some}\:{steps}\:{to}\:{understand}…{you}\:{also} \\ $$$${right}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *