Menu Close

find-a-polynome-solution-of-the-diifferencial-equation-y-y-x-12-

Tinku Tara 0 Comments
Pin




Question Number 33977 by abdo imad last updated on 28/Apr/18
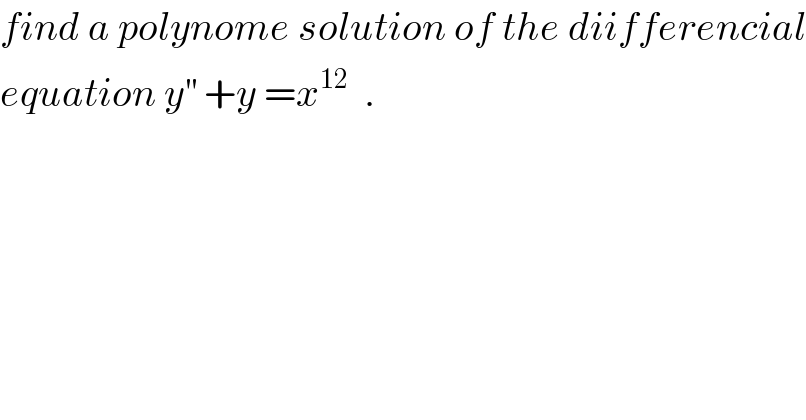
find a polynome solution of the diifferencial equation y^(′′) +y =x^(12) .
$${find}\:{a}\:{polynome}\:{solution}\:{of}\:{the}\:{diifferencial} \\ $$$${equation}\:{y}^{''} \:+{y}\:={x}^{\mathrm{12}} \:\:. \\ $$
Answered by MJS last updated on 28/Apr/18
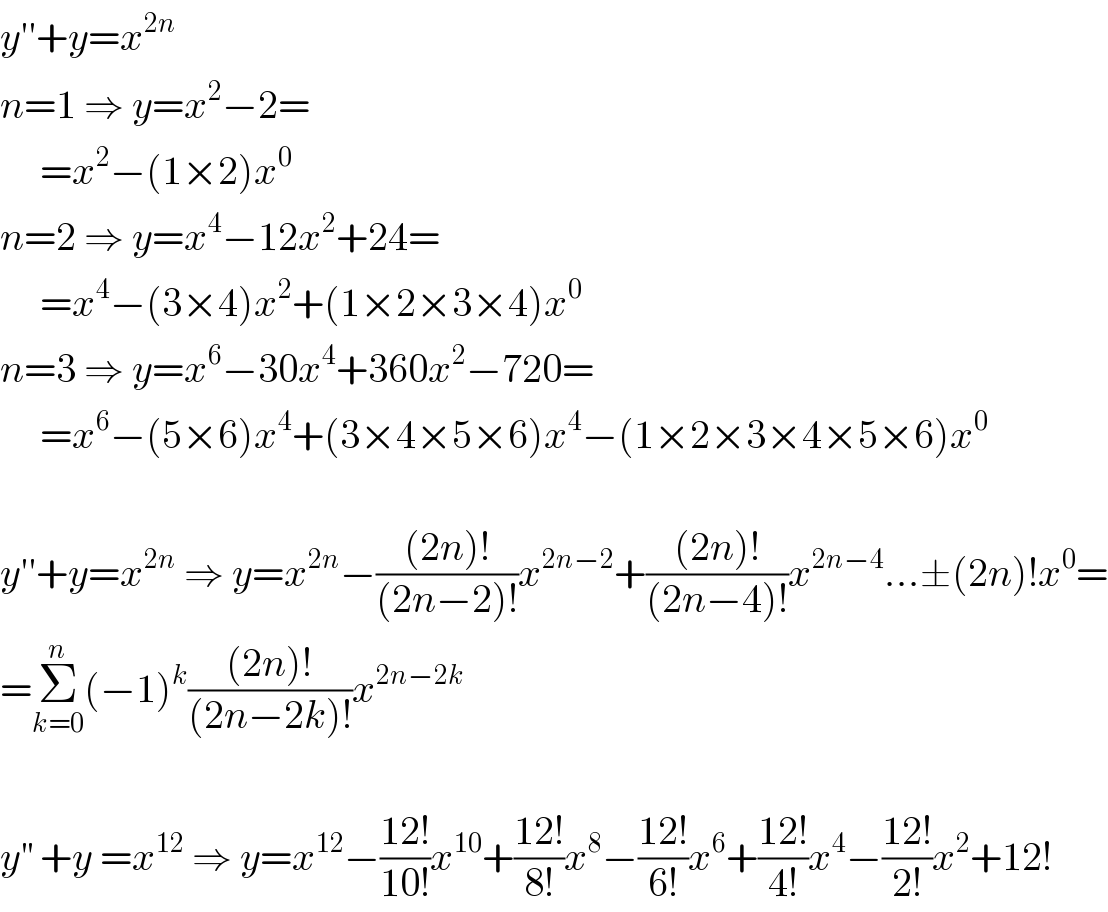
y′′+y=x^(2n) n=1 ⇒ y=x^2 −2= =x^2 −(1×2)x^0 n=2 ⇒ y=x^4 −12x^2 +24= =x^4 −(3×4)x^2 +(1×2×3×4)x^0 n=3 ⇒ y=x^6 −30x^4 +360x^2 −720= =x^6 −(5×6)x^4 +(3×4×5×6)x^4 −(1×2×3×4×5×6)x^0 y′′+y=x^(2n) ⇒ y=x^(2n) −(((2n)!)/((2n−2)!))x^(2n−2) +(((2n)!)/((2n−4)!))x^(2n−4) ...±(2n)!x^0 = =Σ_(k=0) ^n (−1)^k (((2n)!)/((2n−2k)!))x^(2n−2k) y^(′′) +y =x^(12) ⇒ y=x^(12) −((12!)/(10!))x^(10) +((12!)/(8!))x^8 −((12!)/(6!))x^6 +((12!)/(4!))x^4 −((12!)/(2!))x^2 +12!
$${y}''+{y}={x}^{\mathrm{2}{n}} \\ $$$${n}=\mathrm{1}\:\Rightarrow\:{y}={x}^{\mathrm{2}} −\mathrm{2}= \\ $$$$\:\:\:\:\:={x}^{\mathrm{2}} −\left(\mathrm{1}×\mathrm{2}\right){x}^{\mathrm{0}} \\ $$$${n}=\mathrm{2}\:\Rightarrow\:{y}={x}^{\mathrm{4}} −\mathrm{12}{x}^{\mathrm{2}} +\mathrm{24}= \\ $$$$\:\:\:\:\:={x}^{\mathrm{4}} −\left(\mathrm{3}×\mathrm{4}\right){x}^{\mathrm{2}} +\left(\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}\right){x}^{\mathrm{0}} \\ $$$${n}=\mathrm{3}\:\Rightarrow\:{y}={x}^{\mathrm{6}} −\mathrm{30}{x}^{\mathrm{4}} +\mathrm{360}{x}^{\mathrm{2}} −\mathrm{720}= \\ $$$$\:\:\:\:\:={x}^{\mathrm{6}} −\left(\mathrm{5}×\mathrm{6}\right){x}^{\mathrm{4}} +\left(\mathrm{3}×\mathrm{4}×\mathrm{5}×\mathrm{6}\right){x}^{\mathrm{4}} −\left(\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}×\mathrm{6}\right){x}^{\mathrm{0}} \\ $$$$ \\ $$$${y}''+{y}={x}^{\mathrm{2}{n}} \:\Rightarrow\:{y}={x}^{\mathrm{2}{n}} −\frac{\left(\mathrm{2}{n}\right)!}{\left(\mathrm{2}{n}−\mathrm{2}\right)!}{x}^{\mathrm{2}{n}−\mathrm{2}} +\frac{\left(\mathrm{2}{n}\right)!}{\left(\mathrm{2}{n}−\mathrm{4}\right)!}{x}^{\mathrm{2}{n}−\mathrm{4}} …\pm\left(\mathrm{2}{n}\right)!{x}^{\mathrm{0}} = \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \frac{\left(\mathrm{2}{n}\right)!}{\left(\mathrm{2}{n}−\mathrm{2}{k}\right)!}{x}^{\mathrm{2}{n}−\mathrm{2}{k}} \\ $$$$ \\ $$$${y}^{''} \:+{y}\:={x}^{\mathrm{12}} \:\Rightarrow\:{y}={x}^{\mathrm{12}} −\frac{\mathrm{12}!}{\mathrm{10}!}{x}^{\mathrm{10}} +\frac{\mathrm{12}!}{\mathrm{8}!}{x}^{\mathrm{8}} −\frac{\mathrm{12}!}{\mathrm{6}!}{x}^{\mathrm{6}} +\frac{\mathrm{12}!}{\mathrm{4}!}{x}^{\mathrm{4}} −\frac{\mathrm{12}!}{\mathrm{2}!}{x}^{\mathrm{2}} +\mathrm{12}! \\ $$
Commented by MJS last updated on 28/Apr/18
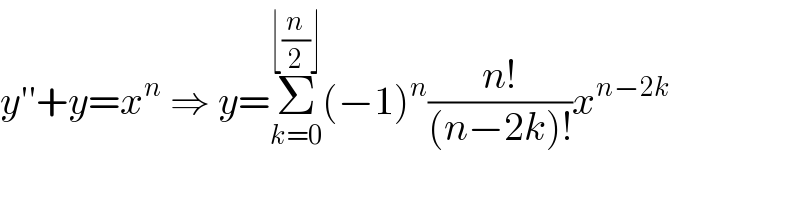
y′′+y=x^n ⇒ y=Σ_(k=0) ^(⌊(n/2)⌋) (−1)^n ((n!)/((n−2k)!))x^(n−2k)
$${y}''+{y}={x}^{{n}} \:\Rightarrow\:{y}=\underset{{k}=\mathrm{0}} {\overset{\lfloor\frac{{n}}{\mathrm{2}}\rfloor} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{n}!}{\left({n}−\mathrm{2}{k}\right)!}{x}^{{n}−\mathrm{2}{k}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *