Menu Close

Find-a-polynomial-f-x-which-satisfy-the-following-conditions-i-f-x-of-degree-4-ii-x-1-is-a-factor-of-f-x-and-f-x-iii-f-0-3-and-f-0-5-iv-when-f-x-is-divided-by-x-2-the-remain

Tinku Tara 0 Comments
Pin




Question Number 105707 by ZiYangLee last updated on 31/Jul/20
Find a polynomial f(x) which satisfy the following conditions: i) f(x) of degree 4 ii) (x−1) is a factor of f(x) and f′(x) iii) f(0)=3 and f′(0)=−5 iv) when f(x) is divided by (x−2), the remainder is 13.
$$\mathrm{Find}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{which}\:\mathrm{satisfy} \\ $$$$\mathrm{the}\:\mathrm{following}\:\mathrm{conditions}: \\ $$$$\left.\mathrm{i}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{of}\:\mathrm{degree}\:\mathrm{4} \\ $$$$\left.\mathrm{ii}\right)\:\left(\mathrm{x}−\mathrm{1}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}'\left(\mathrm{x}\right) \\ $$$$\left.\mathrm{iii}\right)\:\mathrm{f}\left(\mathrm{0}\right)=\mathrm{3}\:\mathrm{and}\:\mathrm{f}'\left(\mathrm{0}\right)=−\mathrm{5} \\ $$$$\left.\mathrm{iv}\right)\:\mathrm{when}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\left(\mathrm{x}−\mathrm{2}\right),\:\mathrm{the} \\ $$$$\:\:\:\:\:\:\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{13}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 31/Jul/20
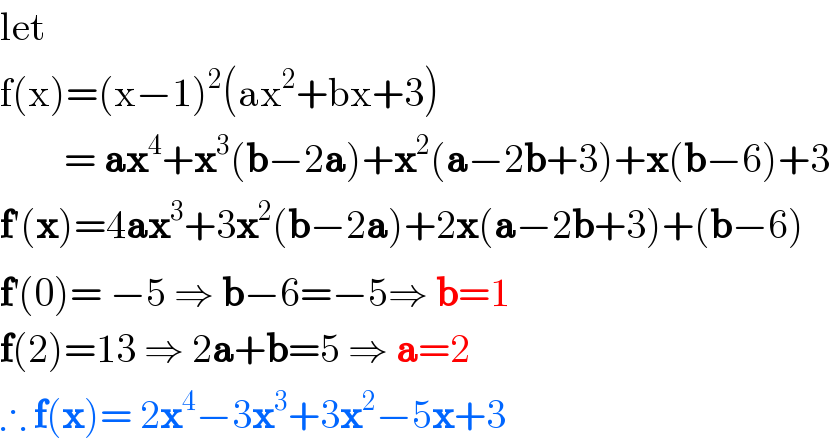
let f(x)=(x−1)^2 (ax^2 +bx+3) = ax^4 +x^3 (b−2a)+x^2 (a−2b+3)+x(b−6)+3 f′(x)=4ax^3 +3x^2 (b−2a)+2x(a−2b+3)+(b−6) f^′ (0)= −5 ⇒ b−6=−5⇒ b=1 f(2)=13 ⇒ 2a+b=5 ⇒ a=2 ∴ f(x)= 2x^4 −3x^3 +3x^2 −5x+3
$$\mathrm{let} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:=\:\boldsymbol{\mathrm{ax}}^{\mathrm{4}} +\boldsymbol{\mathrm{x}}^{\mathrm{3}} \left(\boldsymbol{\mathrm{b}}−\mathrm{2}\boldsymbol{\mathrm{a}}\right)+\boldsymbol{\mathrm{x}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{a}}−\mathrm{2}\boldsymbol{\mathrm{b}}+\mathrm{3}\right)+\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{b}}−\mathrm{6}\right)+\mathrm{3} \\ $$$$\boldsymbol{\mathrm{f}}'\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{4}\boldsymbol{\mathrm{ax}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}−\mathrm{2}\boldsymbol{\mathrm{a}}\right)+\mathrm{2}\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{a}}−\mathrm{2}\boldsymbol{\mathrm{b}}+\mathrm{3}\right)+\left(\boldsymbol{\mathrm{b}}−\mathrm{6}\right) \\ $$$$\boldsymbol{\mathrm{f}}^{'} \left(\mathrm{0}\right)=\:−\mathrm{5}\:\Rightarrow\:\boldsymbol{\mathrm{b}}−\mathrm{6}=−\mathrm{5}\Rightarrow\:\boldsymbol{\mathrm{b}}=\mathrm{1}\:\:\: \\ $$$$\boldsymbol{\mathrm{f}}\left(\mathrm{2}\right)=\mathrm{13}\:\Rightarrow\:\mathrm{2}\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}=\mathrm{5}\:\Rightarrow\:\boldsymbol{\mathrm{a}}=\mathrm{2} \\ $$$$\therefore\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\:\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{\mathrm{x}}+\mathrm{3} \\ $$
Answered by bobhans last updated on 31/Jul/20
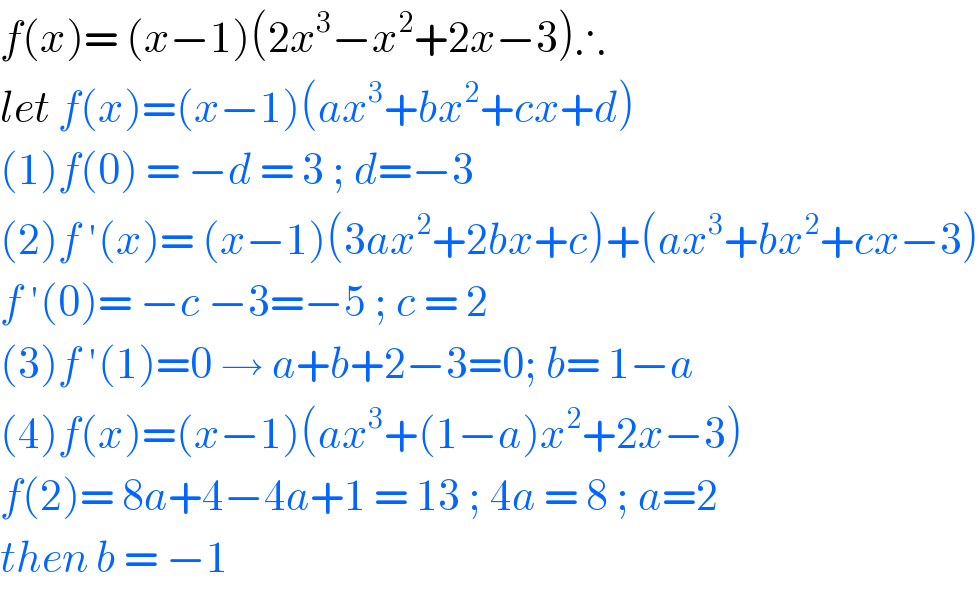
f(x)= (x−1)(2x^3 −x^2 +2x−3)∴ let f(x)=(x−1)(ax^3 +bx^2 +cx+d) (1)f(0) = −d = 3 ; d=−3 (2)f ′(x)= (x−1)(3ax^2 +2bx+c)+(ax^3 +bx^2 +cx−3) f ′(0)= −c −3=−5 ; c = 2 (3)f ′(1)=0 → a+b+2−3=0; b= 1−a (4)f(x)=(x−1)(ax^3 +(1−a)x^2 +2x−3) f(2)= 8a+4−4a+1 = 13 ; 4a = 8 ; a=2 then b = −1
$${f}\left({x}\right)=\:\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}\right)\therefore \\ $$$${let}\:{f}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}\right) \\ $$$$\left(\mathrm{1}\right){f}\left(\mathrm{0}\right)\:=\:−{d}\:=\:\mathrm{3}\:;\:{d}=−\mathrm{3} \\ $$$$\left(\mathrm{2}\right){f}\:'\left({x}\right)=\:\left({x}−\mathrm{1}\right)\left(\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c}\right)+\left({ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}−\mathrm{3}\right) \\ $$$${f}\:'\left(\mathrm{0}\right)=\:−{c}\:−\mathrm{3}=−\mathrm{5}\:;\:{c}\:=\:\mathrm{2}\: \\ $$$$\left(\mathrm{3}\right){f}\:'\left(\mathrm{1}\right)=\mathrm{0}\:\rightarrow\:{a}+{b}+\mathrm{2}−\mathrm{3}=\mathrm{0};\:{b}=\:\mathrm{1}−{a} \\ $$$$\left(\mathrm{4}\right){f}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({ax}^{\mathrm{3}} +\left(\mathrm{1}−{a}\right){x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}\right) \\ $$$${f}\left(\mathrm{2}\right)=\:\mathrm{8}{a}+\mathrm{4}−\mathrm{4}{a}+\mathrm{1}\:=\:\mathrm{13}\:;\:\mathrm{4}{a}\:=\:\mathrm{8}\:;\:{a}=\mathrm{2} \\ $$$${then}\:{b}\:=\:−\mathrm{1} \\ $$
Commented by bemath last updated on 31/Jul/20
cooll ....
$${cooll}\:…. \\ $$
Answered by floor(10²Eta[1]) last updated on 31/Jul/20
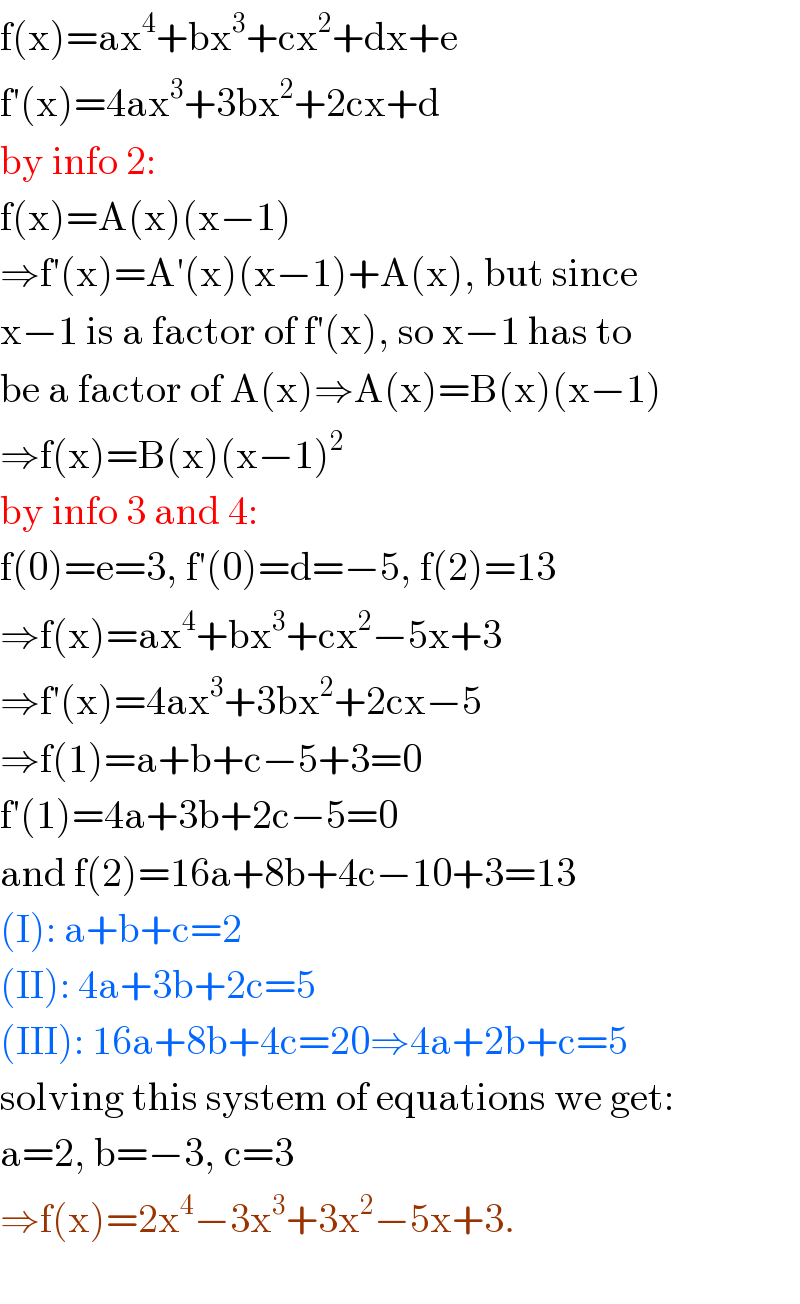
f(x)=ax^4 +bx^3 +cx^2 +dx+e f′(x)=4ax^3 +3bx^2 +2cx+d by info 2: f(x)=A(x)(x−1) ⇒f′(x)=A′(x)(x−1)+A(x), but since x−1 is a factor of f′(x), so x−1 has to be a factor of A(x)⇒A(x)=B(x)(x−1) ⇒f(x)=B(x)(x−1)^2 by info 3 and 4: f(0)=e=3, f′(0)=d=−5, f(2)=13 ⇒f(x)=ax^4 +bx^3 +cx^2 −5x+3 ⇒f′(x)=4ax^3 +3bx^2 +2cx−5 ⇒f(1)=a+b+c−5+3=0 f′(1)=4a+3b+2c−5=0 and f(2)=16a+8b+4c−10+3=13 (I): a+b+c=2 (II): 4a+3b+2c=5 (III): 16a+8b+4c=20⇒4a+2b+c=5 solving this system of equations we get: a=2, b=−3, c=3 ⇒f(x)=2x^4 −3x^3 +3x^2 −5x+3.
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{e} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{4ax}^{\mathrm{3}} +\mathrm{3bx}^{\mathrm{2}} +\mathrm{2cx}+\mathrm{d} \\ $$$$\mathrm{by}\:\mathrm{info}\:\mathrm{2}: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{A}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{A}'\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{A}\left(\mathrm{x}\right),\:\mathrm{but}\:\mathrm{since}\: \\ $$$$\mathrm{x}−\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{f}'\left(\mathrm{x}\right),\:\mathrm{so}\:\mathrm{x}−\mathrm{1}\:\mathrm{has}\:\mathrm{to} \\ $$$$\mathrm{be}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{A}\left(\mathrm{x}\right)\Rightarrow\mathrm{A}\left(\mathrm{x}\right)=\mathrm{B}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{B}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{by}\:\mathrm{info}\:\mathrm{3}\:\mathrm{and}\:\mathrm{4}: \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{e}=\mathrm{3},\:\mathrm{f}'\left(\mathrm{0}\right)=\mathrm{d}=−\mathrm{5},\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{13} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} −\mathrm{5x}+\mathrm{3} \\ $$$$\Rightarrow\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{4ax}^{\mathrm{3}} +\mathrm{3bx}^{\mathrm{2}} +\mathrm{2cx}−\mathrm{5} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{1}\right)=\mathrm{a}+\mathrm{b}+\mathrm{c}−\mathrm{5}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{f}'\left(\mathrm{1}\right)=\mathrm{4a}+\mathrm{3b}+\mathrm{2c}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{16a}+\mathrm{8b}+\mathrm{4c}−\mathrm{10}+\mathrm{3}=\mathrm{13} \\ $$$$\left(\mathrm{I}\right):\:\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{2} \\ $$$$\left(\mathrm{II}\right):\:\mathrm{4a}+\mathrm{3b}+\mathrm{2c}=\mathrm{5} \\ $$$$\left(\mathrm{III}\right):\:\mathrm{16a}+\mathrm{8b}+\mathrm{4c}=\mathrm{20}\Rightarrow\mathrm{4a}+\mathrm{2b}+\mathrm{c}=\mathrm{5} \\ $$$$\mathrm{solving}\:\mathrm{this}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{a}=\mathrm{2},\:\mathrm{b}=−\mathrm{3},\:\mathrm{c}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}^{\mathrm{4}} −\mathrm{3x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{3}. \\ $$$$ \\ $$
Commented by bemath last updated on 31/Jul/20
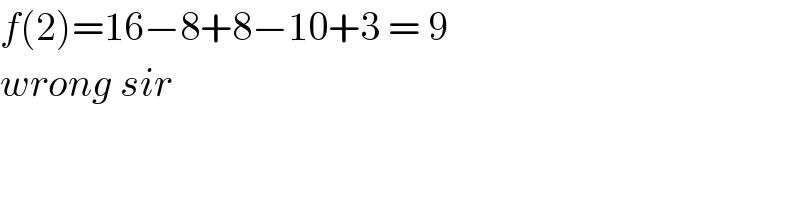
f(2)=16−8+8−10+3 = 9 wrong sir
$${f}\left(\mathrm{2}\right)=\mathrm{16}−\mathrm{8}+\mathrm{8}−\mathrm{10}+\mathrm{3}\:=\:\mathrm{9}\: \\ $$$${wrong}\:{sir}\: \\ $$
Commented by floor(10²Eta[1]) last updated on 31/Jul/20
oh i actually missed the information 4
$$\mathrm{oh}\:\mathrm{i}\:\mathrm{actually}\:\mathrm{missed}\:\mathrm{the}\:\mathrm{information}\:\mathrm{4} \\ $$
Answered by 1549442205PVT last updated on 31/Jul/20
General form of the a polynomyal of degree 4 is f(x)=ax^4 +bx^3 +cx^2 +dx+e.Then f ′(x)=4ax^3 +3bx^2 +2cx+d, From the hypothesis iii)we get: f(0)=3⇔e=3,f ′(0)=−5⇔d=−5.Hence f(x)=ax^4 +bx^3 +cx^2 −5x+3 f ′(x)=4ax^3 +3bx^2 +2cx−5 From ii)we get f(1)=0⇔a+b+c−2=0(1) f ′(1)=0⇔4a+3b+2c−5=0 (2) From iv)we get f(2)=13⇔16a+8b+4c−7=13(3) From(1)(2)and (3) we get { ((a+b+c−2=0)),((4a+3b+2c−5=0)),((16a+8b+4c−7=13)) :}⇔ { ((a+b+c=2 (4))),((4a+3b+2c=5)),((4a+2b+c=5 (6))) :}(5) Substract (5) and (6) we getb+c=0(7), replace in (4) we obtain a=2,replace into (6)we get 2b+c=−3(8).From (7),(8) we obtain b=−3,c=3. Thus,f(x)=2x^4 −3x^3 +3x^2 −5x+3
$$\mathrm{General}\:\mathrm{form}\:\mathrm{of}\:\mathrm{the}\:\mathrm{a}\:\mathrm{polynomyal}\:\mathrm{of}\: \\ $$$$\mathrm{degree}\:\mathrm{4}\:\mathrm{is}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{e}.\mathrm{Then} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{4ax}^{\mathrm{3}} +\mathrm{3bx}^{\mathrm{2}} +\mathrm{2cx}+\mathrm{d}, \\ $$$$\left.\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{iii}\right)\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{3}\Leftrightarrow\mathrm{e}=\mathrm{3},\mathrm{f}\:'\left(\mathrm{0}\right)=−\mathrm{5}\Leftrightarrow\mathrm{d}=−\mathrm{5}.\mathrm{Hence} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} −\mathrm{5x}+\mathrm{3} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{4ax}^{\mathrm{3}} +\mathrm{3bx}^{\mathrm{2}} +\mathrm{2cx}−\mathrm{5} \\ $$$$\left.\mathrm{From}\:\mathrm{ii}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{0}\Leftrightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}−\mathrm{2}=\mathrm{0}\left(\mathrm{1}\right) \\ $$$$\mathrm{f}\:'\left(\mathrm{1}\right)=\mathrm{0}\Leftrightarrow\mathrm{4a}+\mathrm{3b}+\mathrm{2c}−\mathrm{5}=\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$$\left.\mathrm{From}\:\mathrm{iv}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{13}\Leftrightarrow\mathrm{16a}+\mathrm{8b}+\mathrm{4c}−\mathrm{7}=\mathrm{13}\left(\mathrm{3}\right) \\ $$$$\mathrm{From}\left(\mathrm{1}\right)\left(\mathrm{2}\right)\mathrm{and}\:\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{\mathrm{a}+\mathrm{b}+\mathrm{c}−\mathrm{2}=\mathrm{0}}\\{\mathrm{4a}+\mathrm{3b}+\mathrm{2c}−\mathrm{5}=\mathrm{0}}\\{\mathrm{16a}+\mathrm{8b}+\mathrm{4c}−\mathrm{7}=\mathrm{13}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{2}\:\:\:\left(\mathrm{4}\right)}\\{\mathrm{4a}+\mathrm{3b}+\mathrm{2c}=\mathrm{5}}\\{\mathrm{4a}+\mathrm{2b}+\mathrm{c}=\mathrm{5}\:\left(\mathrm{6}\right)}\end{cases}\left(\mathrm{5}\right) \\ $$$$\mathrm{Substract}\:\left(\mathrm{5}\right)\:\mathrm{and}\:\left(\mathrm{6}\right)\:\mathrm{we}\:\mathrm{getb}+\mathrm{c}=\mathrm{0}\left(\mathrm{7}\right), \\ $$$$\mathrm{replace}\:\mathrm{in}\:\left(\mathrm{4}\right)\:\mathrm{we}\:\mathrm{obtain}\:\mathrm{a}=\mathrm{2},\mathrm{replace} \\ $$$$\mathrm{into}\:\left(\mathrm{6}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{2b}+\mathrm{c}=−\mathrm{3}\left(\mathrm{8}\right).\mathrm{From} \\ $$$$\left(\mathrm{7}\right),\left(\mathrm{8}\right)\:\mathrm{we}\:\mathrm{obtain}\:\mathrm{b}=−\mathrm{3},\mathrm{c}=\mathrm{3}. \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{\mathrm{x}}+\mathrm{3} \\ $$
Answered by malwaan last updated on 31/Jul/20
f(x)=ax^4 +bx^3 +cx^2 +dx+e f(1)=a+b+c+d+e=0...1 f′(1)=4a+3b+2c+d=0...2 f(0)=3 ⇒ e=3.....3 f′(0)=−5⇒d=−5....4 f(2)=16a+8b+4c+2d+e=13..5 1⇒a+b+c−5+3=0 ⇒ a+b+c=2....6 2⇒4a+3b+2c−5=0 ⇒ 4a+3b+2c=5....7 5⇒16a+8b+4c−10+3=13 ⇒16a+8b+4c=20 ⇒ 4a+2b+c=5...8 solve the system of equations 6 ; 7 ; 8 we get c = −3 ; b = 3 ; a = 2 the polynomial is f(x)= 2x^4 −3x^3 +3x^2 −5x+3
$${f}\left({x}\right)={ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${f}\left(\mathrm{1}\right)={a}+{b}+{c}+{d}+{e}=\mathrm{0}…\mathrm{1} \\ $$$${f}'\left(\mathrm{1}\right)=\mathrm{4}{a}+\mathrm{3}{b}+\mathrm{2}{c}+{d}=\mathrm{0}…\mathrm{2} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{3}\:\Rightarrow\:{e}=\mathrm{3}…..\mathrm{3} \\ $$$${f}'\left(\mathrm{0}\right)=−\mathrm{5}\Rightarrow{d}=−\mathrm{5}….\mathrm{4} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{16}{a}+\mathrm{8}{b}+\mathrm{4}{c}+\mathrm{2}{d}+{e}=\mathrm{13}..\mathrm{5} \\ $$$$\mathrm{1}\Rightarrow{a}+{b}+{c}−\mathrm{5}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\:\:{a}+{b}+{c}=\mathrm{2}….\mathrm{6} \\ $$$$\mathrm{2}\Rightarrow\mathrm{4}{a}+\mathrm{3}{b}+\mathrm{2}{c}−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{4}{a}+\mathrm{3}{b}+\mathrm{2}{c}=\mathrm{5}….\mathrm{7} \\ $$$$\mathrm{5}\Rightarrow\mathrm{16}{a}+\mathrm{8}{b}+\mathrm{4}{c}−\mathrm{10}+\mathrm{3}=\mathrm{13} \\ $$$$\Rightarrow\mathrm{16}{a}+\mathrm{8}{b}+\mathrm{4}{c}=\mathrm{20} \\ $$$$\Rightarrow\:\mathrm{4}{a}+\mathrm{2}{b}+{c}=\mathrm{5}…\mathrm{8} \\ $$$${solve}\:{the}\:{system}\:{of}\:{equations} \\ $$$$\mathrm{6}\:\:;\:\mathrm{7}\:;\:\mathrm{8}\:{we}\:{get} \\ $$$${c}\:=\:−\mathrm{3}\:\:;\:{b}\:=\:\mathrm{3}\:;\:{a}\:=\:\mathrm{2} \\ $$$${the}\:{polynomial}\:{is} \\ $$$${f}\left({x}\right)=\:\mathrm{2}{x}^{\mathrm{4}} \:−\mathrm{3}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} \:−\mathrm{5}{x}+\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *