Question Number 93299 by Rio Michael last updated on 12/May/20
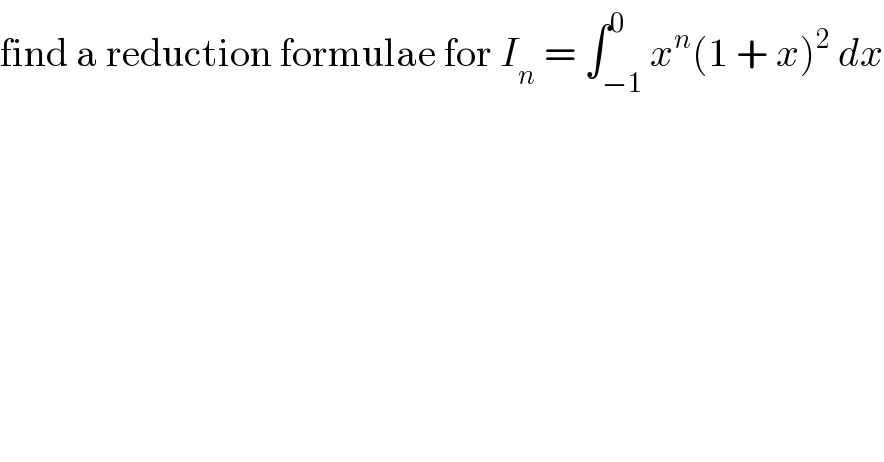
$$\mathrm{find}\:\mathrm{a}\:\mathrm{reduction}\:\mathrm{formulae}\:\mathrm{for}\:{I}_{{n}} \:=\:\int_{−\mathrm{1}} ^{\mathrm{0}} {x}^{{n}} \left(\mathrm{1}\:+\:{x}\right)^{\mathrm{2}} \:{dx} \\ $$
Commented by mathmax by abdo last updated on 12/May/20
![I_n =∫_(−1) ^0 x^n (1+x)^2 dx ⇒I_n =_(x=−t) ∫_0 ^1 (−1)^n t^n (1−t)^2 dt =(−1)^n ∫_0 ^1 t^n (t−1)^2 dt by parts we get ∫_0 ^1 t^n (t−1)^2 dt =[(1/(n+1))t^(n+1) (t−1)^2 ]_0 ^1 −(2/(n+1))∫_0 ^1 t^(n+1) (t−1)dt =−(2/(n+1)) { [(1/(n+2))t^(n+2) (t−1)]_0 ^1 −(1/(n+2))∫_0 ^1 t^(n+2) dt} =−(2/(n+1))(−(1/(n+2)))×(1/(n+3)) =(2/((n+1)(n+2)(n+3))) ⇒ I_n =((2(−1)^n )/((n+1)(n+2)(n+3)))](https://www.tinkutara.com/question/Q93358.png)
$${I}_{{n}} =\int_{−\mathrm{1}} ^{\mathrm{0}} \:{x}^{{n}} \left(\mathrm{1}+{x}\right)^{\mathrm{2}} \:{dx}\:\Rightarrow{I}_{{n}} =_{{x}=−{t}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} \:{t}^{{n}} \left(\mathrm{1}−{t}\right)^{\mathrm{2}} \:{dt} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} \left({t}−\mathrm{1}\right)^{\mathrm{2}} {dt}\:\:{by}\:{parts}\:{we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} \left({t}−\mathrm{1}\right)^{\mathrm{2}} {dt}\:=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \left({t}−\mathrm{1}\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{\mathrm{2}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}+\mathrm{1}} \:\left({t}−\mathrm{1}\right){dt} \\ $$$$=−\frac{\mathrm{2}}{{n}+\mathrm{1}}\:\left\{\:\:\left[\frac{\mathrm{1}}{{n}+\mathrm{2}}{t}^{{n}+\mathrm{2}} \left({t}−\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{\mathrm{1}}{{n}+\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}+\mathrm{2}} \:{dt}\right\} \\ $$$$=−\frac{\mathrm{2}}{{n}+\mathrm{1}}\left(−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)×\frac{\mathrm{1}}{{n}+\mathrm{3}}\:=\frac{\mathrm{2}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\:\Rightarrow \\ $$$${I}_{{n}} =\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$
Commented by Rio Michael last updated on 12/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
