Menu Close

find-a-relation-betwen-x-2-and-x-2-

Tinku Tara 0 Comments
Pin




Question Number 49639 by maxmathsup by imad last updated on 08/Dec/18
find a relation betwen [x]^2 and [−x]^2
findarelationbetwen[x]2and[−x]2
Commented by Abdo msup. last updated on 23/Dec/18
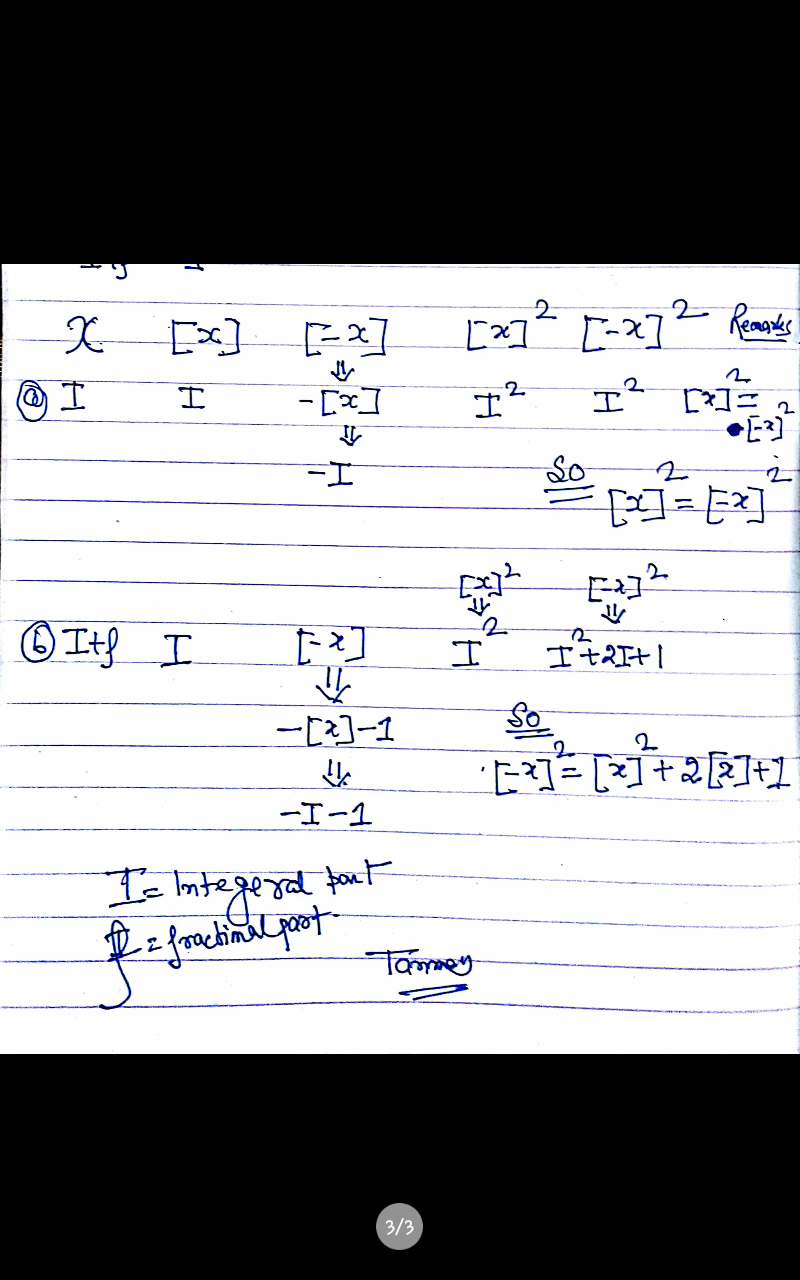
if x∈Z [x]^2 =x^2 and [−x]^2 =(−x)^2 =x^2 ⇒ [x]^2 =[−x]^2 if x∈R−Z let [x]=p ⇒p<x<p+1 ⇒ −p−1<−x<−p ⇒[−x]=−p−1=−1−[x] ⇒ [−x]^2 =(1+[x])^2 =1+2[x] +[x]^2 .
ifx∈Z[x]2=x2and[−x]2=(−x)2=x2⇒[x]2=[−x]2ifx∈R−Zlet[x]=p⇒p<x<p+1⇒−p−1<−x<−p⇒[−x]=−p−1=−1−[x]⇒[−x]2=(1+[x])2=1+2[x]+[x]2.
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Dec/18

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *