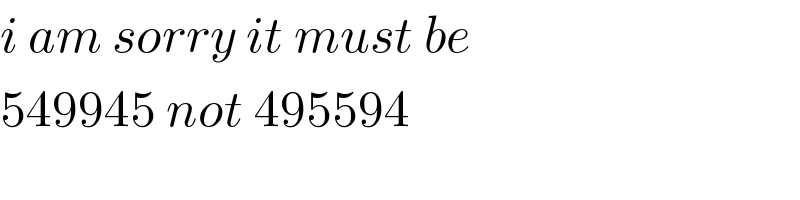find-all-6-digit-numbers-which-are-not-only-palindrome-but-also-divisible-by-495-

Question Number 83910 by redmiiuser last updated on 07/Mar/20

find all 6 digit numbers which are not

only palindrome but also divisible by 495 .

Commented by redmiiuser last updated on 08/Mar/20

CAN ANYONE

ANSWER THIS

QUESTION .

Answered by Kunal12588 last updated on 08/Mar/20

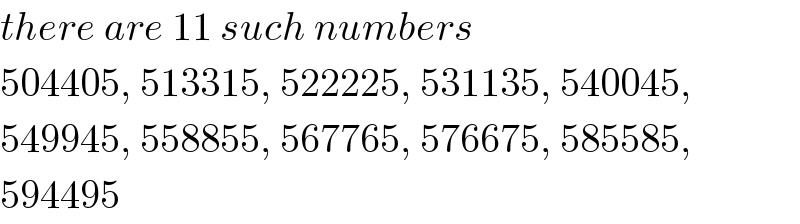
t h e r e a r e 11 s u c h n u m b e r s

504405, 513315, 522225, 531135, 540045,

549945, 558855, 567765, 576675, 585585,

594495

Commented by redmiiuser last updated on 08/Mar/20

G R E A T

Commented by naka3546 last updated on 08/Mar/20

S h o w y o u r w o r k i n g s, p l e a s e .

Commented by Kunal12588 last updated on 08/Mar/20

i {d o n}^{'} t t h i n k i c a n f i n d i t w i t h a n y m e t h o d .

I j u s t u s e d t h e b r u t e f o r c e m e t h o d .

Answered by redmiiuser last updated on 08/Mar/20

t h e r e i s a n e a s y w a y

w e k n o w

495 = 9 \times 5 \times 11

a s t h e n u m b e r m u s t

b e d i v i s i b l e b y 495 h e n c e

s o b y 9 a n d 5 a n d 11 .

t o b e d i v i s i b l e b y 5

t h e l a s t d i g h t m u s t b e

5 a n d n o t 0 .

a g a i n f o r 9 t h e s u m o f

t h e d i g h t s m u s t b e d i v i s i 6 l e

b y 9 .

n o w f o r 11 l e t s t a k e

a n e x a m p l e .

594495

h e r e t h e n u m b e r i s

d i v i s i b l e b y 5 a n d 9 .

b u t t h e n u m b e r i s d i v i s i b l e

b y 11 o n a p p l y i n g t h e

d i v i s i b l i t y t r i c k i g e t t h i s .

a g a i n i n 495594

t h e n u m b e r i s d i v i s i b l e b y

11 a n d 5 a n d 9 .

b u t t h e c h a n g e i s

t h e t e r m i n a l n u m b e r s

a r e d e c r e a s e d b y 1

w h i l e m i d d l e o n e s

a r e i n c r e a s e d b y 1 .

h e n c e b y a p p l y i n g

t h i s c o n c e p t w e c a n s o l v e

Commented by redmiiuser last updated on 08/Mar/20

i a m s o r r y i t m u s t b e

549945 n o t 495594