find-all-asymptotes-of-function-f-x-x-2-4x-5-x-2-x-3-x-5-

Question Number 113952 by bemath last updated on 16/Sep/20

f i n d a l l a s y m p t o t e s o f f u n c t i o n

f (x) = {(\frac{x^{2} + 4 x - 5}{x^{2} + x + 3})}^{x + 5}

Commented by MJS_new last updated on 16/Sep/20

forgot the squares ? ? ?

Commented by bemath last updated on 16/Sep/20

y e s s i r . s o r r y

Commented by MJS_new last updated on 16/Sep/20

if {it}^{'} s

f (x) = {(\frac{x^{2} + 4 x - 5}{x^{2} + x + 3})}^{x + 5}

I get \lim_{x \to \pm \infty} f (x) = e^{3}

\Rightarrow horizontal asymptote y = e^{3}

for the rest I^{'} m not sure as we still get some

real solutions for \frac{x^{2} + 4 x - 5}{x^{2} + x + 3} < 0

Commented by MJS_new last updated on 16/Sep/20

\dots there is a vertical asymptote x = - 5

Answered by 1549442205PVT last updated on 16/Sep/20

we find horizontal asymptote :

y = \underset{x \to \infty}{limf (x)} = \lim_{x \to \infty} {(1 + \frac{3 x - 8}{x^{2} + x + 3})}^{x + 5}

= \lim_{x \to \infty} (1 + \frac{1}{\frac{x^{2} + x + 3}{3 x - 8}}) \frac{x^{2} + x + 3}{3 x - 8} . (\frac{(3 x - 8) (x + 5)}{x^{2} + x + 3})

= e^{\lim_{x \to \infty} \frac{{3 x}^{2} + 7 x - 40}{x^{2} + x + 3}} = e^{\lim_{x \to \infty} (3 + \frac{4 x - 49}{x^{2} + x + 3})}

= e^{3} since \lim_{x \to \infty} (3 + \frac{4 x - 49}{x^{2} + x + 3}) = 3

Therefore graph of function

f (x) = {(\frac{x^{2} + 4 x - 5}{x^{2} + x + 3})}^{x + 5} has the

horizontal asymptote y = e^{3}

Answered by bobhans last updated on 16/Sep/20

(1) h o r i z o n t a l a s y m p t o t e s

y = \lim_{x \to \pm \infty} f (x) = \lim_{x \to \pm \infty} {(\frac{x^{2} + 4 x - 5}{x^{2} + x + 3})}^{x + 5}

= e^{\lim_{x \to \pm \infty} (\frac{x^{2} + 4 x - 5}{x^{2} + x + 3} - 1) . (x + 5)}

= e^{\lim_{x \to \pm \infty} (\frac{(3 x - 8) (x + 5)}{x^{2} + x + 3})} = e^{3}

(2) v e r t i c a l a s y m p t o t e s

\lim_{x \to a} f (x) = \pm \infty . w e a p l l y f o r m u l a

I f f (x) = {(\frac{h (x)}{g (x)})}^{u (x)}; v e r t i c a l a s y m p t o t e s

w e g e t f r o m h (x) = 0, i n t h i s c a s e

h (x) = x^{2} + 4 x - 5 = (x + 5) (x - 1) = 0

s o t h e v e r t i c a l a s y m p t o t e s i s x = - 5 \land x = 1

Commented by MJS_new last updated on 16/Sep/20

but f (1) = 0 is defined, so {there}^{'} s no asymptote

Commented by bobhans last updated on 16/Sep/20

h o w a b o u t f (- 5) s i r ?

o o f (- 5) = 0^{0} s i r . y e s x = - 5 i s

v e r t i c a l a s y m p t o t e s

Commented by bobhans last updated on 16/Sep/20

Commented by bobhans last updated on 16/Sep/20

i a p p l y g e o g e b r a . t h i s g r a p h

Commented by MJS_new last updated on 16/Sep/20

f (- 5) = {(\frac{0}{17})}^{0} = 0^{0} which is not defined

many graphic calculators use 0^{0} = 1 and in

this case \lim_{x \to - 5} f (x) = 1 \Rightarrow different situation

from f (1) = 0

we would also not say y = x^{2} has an asymptote

y = 0, would we ?

Commented by bemath last updated on 16/Sep/20

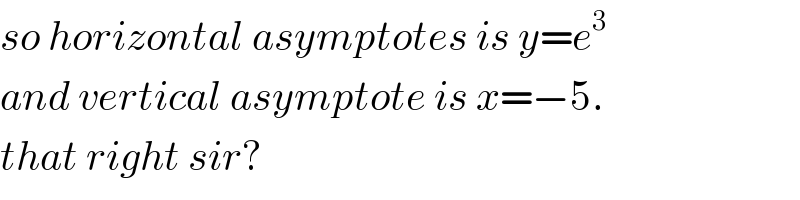
s o h o r i z o n t a l a s y m p t o t e s i s y = e^{3}

a n d v e r t i c a l a s y m p t o t e i s x = - 5 .

t h a t r i g h t s i r ?

Commented by MJS_new last updated on 16/Sep/20

yes in my opinion .

Commented by bemath last updated on 16/Sep/20

t h a n k y o u s i r . i a g r e e

Facebook Tweet Pin