Find-all-complex-number-z-that-satisfy-sinh-z-i-

Question Number 57719 by Joel578 last updated on 10/Apr/19

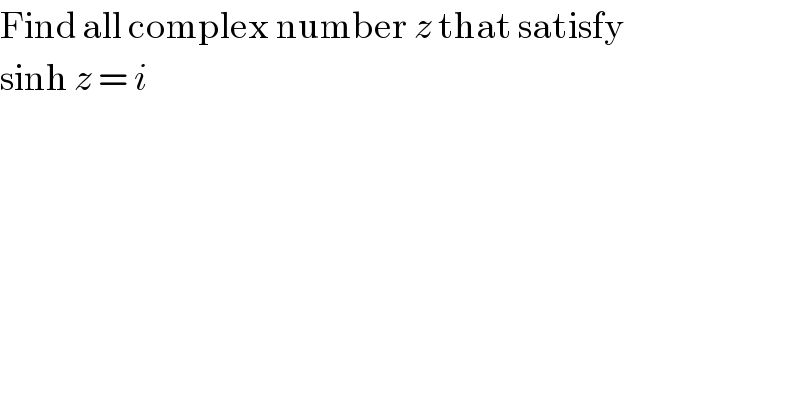
Find all complex number z that satisfy

\sinh z = i

Answered by mr W last updated on 10/Apr/19

\sinh z = \frac{e^{z} - e^{- z}}{2} = i

\Rightarrow {(e^{z})}^{2} - 2 i (e^{z}) - 1 = 0

\Rightarrow {(e^{z} - i)}^{2} = 0

\Rightarrow e^{z} = i = \cos (2 n π + \frac{π}{2}) + i \sin (2 n π + \frac{π}{2}) = e^{(2 n π + \frac{π}{2}) i}

\Rightarrow z = (2 n π + \frac{π}{2}) i

Facebook Tweet Pin