Question Number 151453 by mathdanisur last updated on 21/Aug/21

Commented by MJS_new last updated on 21/Aug/21

Commented by mathdanisur last updated on 21/Aug/21

Commented by MJS_new last updated on 21/Aug/21
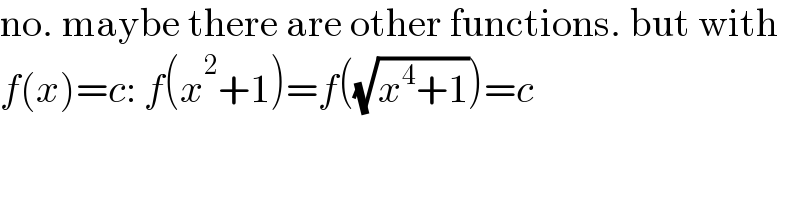
Commented by mathdanisur last updated on 22/Aug/21

Commented by MJS_new last updated on 22/Aug/21
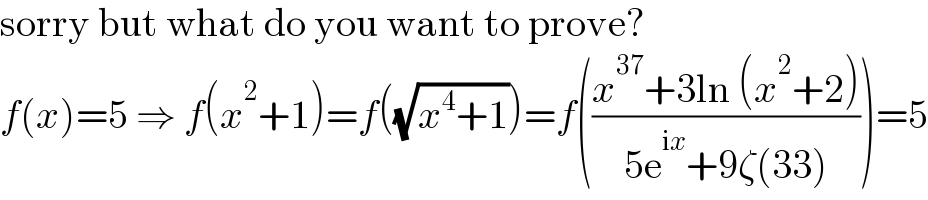
Commented by mathdanisur last updated on 22/Aug/21
Commented by MJS_new last updated on 22/Aug/21

