Menu Close

find-all-integers-n-for-which-13-4-n-2-1-

Tinku Tara 0 Comments
Pin




Question Number 94097 by Rio Michael last updated on 16/May/20
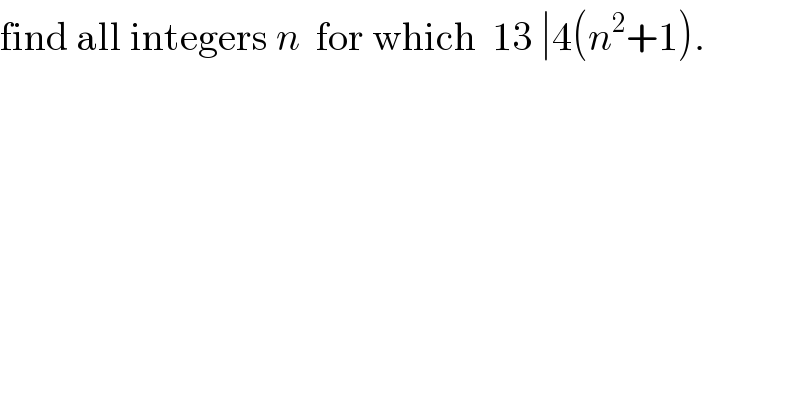
find all integers n for which 13 ∣4(n^2 +1).
$$\mathrm{find}\:\mathrm{all}\:\mathrm{integers}\:{n}\:\:\mathrm{for}\:\mathrm{which}\:\:\mathrm{13}\:\mid\mathrm{4}\left({n}^{\mathrm{2}} +\mathrm{1}\right). \\ $$
Commented by Rasheed.Sindhi last updated on 17/May/20
This s equivalent to: 13 ∣(n^2 +1) ((n^2 +1)/(13))=k⇒13k−1=n^2 All k′s for which 13k−1 is perfect square. Some values of k: k=2,5,25,34,74,89,... n=5,8,18,21,31,34,44,... General solutions: n=13q+5,13q+8 ∀ q∈Z ..... ...
$${This}\:{s}\:{equivalent}\:{to}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{13}\:\mid\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\frac{{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{13}}={k}\Rightarrow\mathrm{13}{k}−\mathrm{1}={n}^{\mathrm{2}} \\ $$$${All}\:{k}'{s}\:{for}\:{which}\:\mathrm{13}{k}−\mathrm{1}\:{is} \\ $$$${perfect}\:{square}. \\ $$$${Some}\:{values}\:{of}\:{k}: \\ $$$${k}=\mathrm{2},\mathrm{5},\mathrm{25},\mathrm{34},\mathrm{74},\mathrm{89},… \\ $$$${n}=\mathrm{5},\mathrm{8},\mathrm{18},\mathrm{21},\mathrm{31},\mathrm{34},\mathrm{44},… \\ $$$$\mathcal{G}{eneral}\:{solutions}: \\ $$$${n}=\mathrm{13}{q}+\mathrm{5},\mathrm{13}{q}+\mathrm{8}\:\:\:\:\forall\:{q}\in\mathbb{Z}\:\:\: \\ $$$$….. \\ $$$$… \\ $$
Answered by Rasheed.Sindhi last updated on 17/May/20
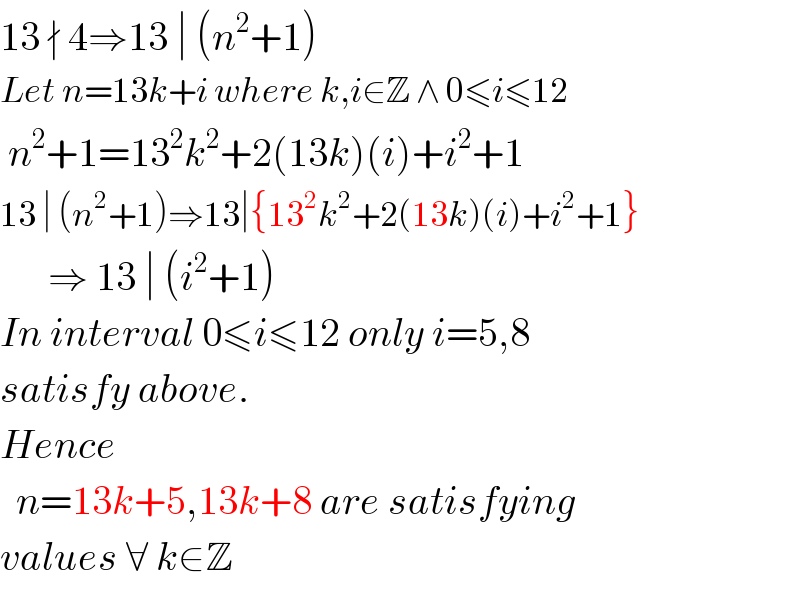
13 ∤ 4⇒13 ∣ (n^2 +1) Let n=13k+i where k,i∈Z ∧ 0≤i≤12 n^2 +1=13^2 k^2 +2(13k)(i)+i^2 +1 13 ∣ (n^2 +1)⇒13∣{13^2 k^2 +2(13k)(i)+i^2 +1} ⇒ 13 ∣ (i^2 +1) In interval 0≤i≤12 only i=5,8 satisfy above. Hence n=13k+5,13k+8 are satisfying values ∀ k∈Z
$$\mathrm{13}\:\nmid\:\mathrm{4}\Rightarrow\mathrm{13}\:\mid\:\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${Let}\:{n}=\mathrm{13}{k}+{i}\:{where}\:{k},{i}\in\mathbb{Z}\:\wedge\:\mathrm{0}\leqslant{i}\leqslant\mathrm{12} \\ $$$$\:{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{13}^{\mathrm{2}} {k}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{13}{k}\right)\left({i}\right)+{i}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{13}\:\mid\:\left({n}^{\mathrm{2}} +\mathrm{1}\right)\Rightarrow\mathrm{13}\mid\left\{\mathrm{13}^{\mathrm{2}} {k}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{13}{k}\right)\left({i}\right)+{i}^{\mathrm{2}} +\mathrm{1}\right\} \\ $$$$\:\:\:\:\:\:\Rightarrow\:\mathrm{13}\:\mid\:\left({i}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${In}\:{interval}\:\mathrm{0}\leqslant{i}\leqslant\mathrm{12}\:{only}\:{i}=\mathrm{5},\mathrm{8} \\ $$$${satisfy}\:{above}. \\ $$$${Hence}\: \\ $$$$\:\:{n}=\mathrm{13}{k}+\mathrm{5},\mathrm{13}{k}+\mathrm{8}\:{are}\:{satisfying} \\ $$$${values}\:\forall\:{k}\in\mathbb{Z} \\ $$
Answered by Rasheed.Sindhi last updated on 17/May/20
13 ∣4(n^2 +1) is aquivalent to: 13 ∣(n^2 +1) ^• n:13k,13k+1,...,13k+4,13k+5, 13k+6,13k+7,13k+8,13k+9, ...,13k+12 ^• For values of n written in black We can easily prove that: 13 ∤ (n^2 +1) For example if n=13k+2 n^2 +1=13^2 k^2 +2.13k.2+5 =13(13k^2 +4k)+5 ∴ 13 ∤ (n^2 +1) ^• For values of n written in red We can easily prove that: 13 ∣ (n^2 +1) For an example if n=13k+8 n^2 +1=13^2 k^2 +2.13k.8+65 =13(13k^2 +16k+5) ∴ 13 ∣ (n^2 +1) ^• Hence13 ∣ (n^2 +1) for only 13k+5 & 13k+8
$$\mathrm{13}\:\mid\mathrm{4}\left({n}^{\mathrm{2}} +\mathrm{1}\right)\:{is}\:{aquivalent}\:{to}: \\ $$$$\:\:\:\:\:\:\:\mathrm{13}\:\mid\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:^{\bullet} {n}:\mathrm{13}{k},\mathrm{13}{k}+\mathrm{1},…,\mathrm{13}{k}+\mathrm{4},\mathrm{13}{k}+\mathrm{5}, \\ $$$$\:\:\:\:\:\:\mathrm{13}{k}+\mathrm{6},\mathrm{13}{k}+\mathrm{7},\mathrm{13}{k}+\mathrm{8},\mathrm{13}{k}+\mathrm{9}, \\ $$$$\:\:\:\:\:\:…,\mathrm{13}{k}+\mathrm{12} \\ $$$$\:^{\bullet} \mathcal{F}{or}\:{values}\:{of}\:{n}\:{written}\:{in}\:{black} \\ $$$${We}\:{can}\:{easily}\:{prove}\:{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{13}\:\nmid\:\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:\:{For}\:{example}\:{if}\:{n}=\mathrm{13}{k}+\mathrm{2} \\ $$$$\:\:\:\:{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{13}^{\mathrm{2}} {k}^{\mathrm{2}} +\mathrm{2}.\mathrm{13}{k}.\mathrm{2}+\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{13}\left(\mathrm{13}{k}^{\mathrm{2}} +\mathrm{4}{k}\right)+\mathrm{5} \\ $$$$\:\:\:\:\therefore\:\mathrm{13}\:\nmid\:\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:^{\bullet} \mathcal{F}{or}\:{values}\:{of}\:{n}\:{written}\:{in}\:{red} \\ $$$${We}\:{can}\:{easily}\:{prove}\:{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{13}\:\mid\:\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:{For}\:{an}\:{example}\:{if}\:{n}=\mathrm{13}{k}+\mathrm{8} \\ $$$$\:\:\:\:\:{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{13}^{\mathrm{2}} {k}^{\mathrm{2}} +\mathrm{2}.\mathrm{13}{k}.\mathrm{8}+\mathrm{65} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{13}\left(\mathrm{13}{k}^{\mathrm{2}} +\mathrm{16}{k}+\mathrm{5}\right) \\ $$$$\:\:\:\:\:\therefore\:\:\mathrm{13}\:\mid\:\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:^{\bullet} \mathcal{H}{ence}\mathrm{13}\:\mid\:\left({n}^{\mathrm{2}} +\mathrm{1}\right)\:{for}\:{only} \\ $$$$\mathrm{13}{k}+\mathrm{5}\:\&\:\mathrm{13}{k}+\mathrm{8} \\ $$
Commented by Rio Michael last updated on 17/May/20
thank you sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *